Đề thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 6

Đề bài

Phần trắc nghiệm (7 điểm)

Câu 1: Chọn câu trả lời đúng.

Câu 2: Mệnh đề “Tồn tại một số thực mà lập phương của nó bằng 10” được viết lại là:

Câu 3: Chọn khẳng định sai:

A. Mệnh đề P có mệnh đề phủ định là $\overline P$, nếu P đúng thì $\overline P$ sai

B. Mệnh đề P có mệnh đề phủ định là $\overline P$, $\overline P$ đúng thì chưa khẳng định được P sai

C. Mệnh đề phủ định của mệnh đề P là mệnh đề không phải P, kí hiệu là $\overline P$

D. Mệnh đề P có mệnh đề phủ định là $\overline P$, nếu P sai thì $\overline P$ đúng

Câu 4: Tập hợp nào dưới đây cho bằng cách liệt kê các phần tử của tập hợp:

Câu 5: Tập hợp C gồm các số tự nhiên lẻ. Viết tập hợp C bằng cách chỉ ra tính chất đặc trưng của các phần tử.

Câu 6: Tập hợp A gồm các chữ cái trong từ “NHA TRANG” là:

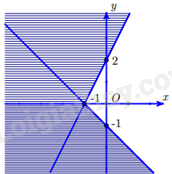
Câu 7: Miền nghiệm của một hệ bất phương trình là miền không bị gạch chéo (tính cả bờ) như hình dưới. Điểm nào sau đây nằm trong miền nghiệm của hệ bất phương trình trên?

Câu 8: Trong các hệ bất phương trình dưới đây, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?

Câu 9: Hệ bất phương trình $\left\{ \begin{array}{l}x + y > 0\\2x + 5y < 0\end{array} \right.$ có tập nghiệm là S. Khẳng định nào sau đây đúng?

Câu 10: Miền nghiệm của bất phương trình $- x + y > 1$ là:

A. Nửa mặt phẳng không kể bờ $d: - x + y = 1$ chứa điểm O (0; 0)

B. Nửa mặt phẳng bờ $d: - x + y = 1$ chứa điểm O (0; 0)

C. Nửa mặt phẳng bờ $d: - x + y = 1$ không chứa điểm O (0; 0)

D. Nửa mặt phẳng không kể bờ $d: - x + y = 1$ không chứa điểm O (0; 0)

Câu 11: Trong các bất phương trình sau, bất phương trình nào không là bất phương trình bậc nhất hai ẩn?

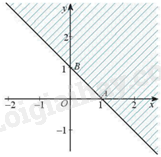
Câu 12: Cho bất phương trình có miền nghiệm là phần không bị gạch chéo (không tính bờ) như hình dưới. Điểm nào sau đây nằm trong miền nghiệm của bất phương trình trên?

Câu 13: Với ${0^0} \le \alpha  \le {180^0}$ thì:

Câu 14: Nếu $\alpha$ là góc nhọn thì:

Câu 15: Với $\alpha  \ne {90^0}$, thì:

Câu 16: Giá trị của biểu thức $A = \sin {30^0} + \cos {60^0}$ là:

Câu 17: Cho tam giác ABC có $AB = c,BC = a,AC = b$. Khi đó:

Câu 18: Cho tam giác ABC có $AC = 40cm,\widehat B = {45^0}$. Bán kính của đường tròn ngoại tiếp tam giác ABC là:

Câu 19: Cho tam giác ABC có $AB = 5cm,BC = 6cm,\widehat B = {45^0}.$ Diện tích tam giác ABC là:

Câu 20: Cho tam giác ABC có $AB = c,BC = a,AC = b$, $p = \frac{{a + b + c}}{2}$. Diện tích S của tam giác ABC là:

A. $S = p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)$

B. $S = \frac{1}{2}p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)$

C. $S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

D. $S = \frac{1}{2}\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

Câu 21: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. 2020 là số chia hết cho 3

B. $\pi  > 3,15$

C. Tam giác có hai góc bằng nhau là tam giác đều

D. Tam giác có hai góc bằng ${45^0}$ là tam giác vuông cân 

Câu 22: Cho mệnh đề: “Nghiệm của phương trình ${x^2} - 10 = 0$ là số vô tỉ”. Mệnh đề phủ định của mệnh đề trên là:

A. “Nghiệm của phương trình ${x^2} - 10 = 0$ không là số vô tỉ”

B. “Nghiệm của phương trình ${x^2} - 10 = 0$ là không số hữu tỉ”

C.  “Phương trình ${x^2} - 10 = 0$ vô nghiệm”

D. “Nghiệm của phương trình ${x^2} - 10 = 0$ không là số nguyên”

Câu 23: Cho số tự nhiên n. Xét mệnh đề: “Nếu n chia hết cho 16 thì n chia hết cho 4”. Mệnh đề đảo của mệnh đề đó là:

A. Nếu n chia hết cho 16 thì n không chia hết cho 4

B. Nếu n chia hết cho 4 thì n chia hết cho 16

C. Nếu n chia hết cho 4 thì n không chia hết cho 16

D. Nếu n không chia hết cho 16 thì n không chia hết cho 4

Câu 24: Tập hợp $A = \left\{ {x \in \mathbb{R}|x < 2} \right\}$ được biểu diễn trên trục số là:

Câu 25: Cho các tập hợp $A = \left\{ {1;\;2;\;3} \right\}$, $B = \left\{ {2;\;3;\;4} \right\}$, $C = \left\{ {1;2;3;4} \right\}$. Chọn khẳng định đúng.

Câu 26: Chọn đáp án đúng:

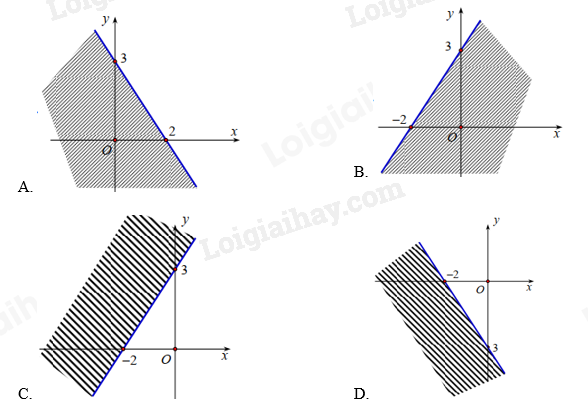
Câu 27: Cho bất phương trình: $6x + 4y - 3 > 9$. Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng tọa độ là:

Câu 28: Miền nghiệm của bất phương trình $3x - 2y + 6 < 0$ là:

Câu 29: Cho hình vẽ sau:

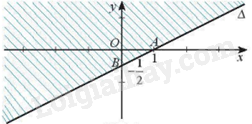
Miền không gạch chéo (không kể đường thẳng $\Delta$) là miền nghiệm của bất phương trình nào dưới đây:

Câu 30: Cho hệ bất phương trình $\left\{ \begin{array}{l}x - 2y \ge  - 2\\7x - 4y \le 16\\2x + y \ge  - 4\end{array} \right.$. Giá trị nhỏ nhất của biểu thức $F\left( {x;y} \right) = 3x - y$ với (x; y) thỏa mãn hệ bất phương trình trên là:

Câu 31: Cho tam giác ABC. Khẳng định nào sau đây đúng?

Câu 32: Cho góc $\alpha \left( {{0^0} < \alpha  < {{180}^0},\alpha  \ne {{90}^0}} \right)$ thỏa mãn $\tan \alpha  = 2$. Giá trị của biểu thức $P = \frac{{2\sin \alpha  - 3\cos \alpha }}{{3\sin \alpha  + 2\cos \alpha }}$ là:

Câu 33: Cho tam giác ABC có $AB = 6cm,AC = 5cm,BC = 8cm$. Số đo góc A là (làm tròn đến hàng phần trăm)

Câu 34: Cho tam giác ABC có $AB = 13cm,BC = 14cm,AC = 15cm$. Bán kính đường tròn ngoại tiếp tam giác ABC là:

Câu 35: Cho tam giác ABC có diện tích bằng $10\sqrt 3 c{m^2}$ và chu vi của tam giác bằng 20cm. Bán kính đường tròn nội tiếp r của tam giác trên là:

Phần tự luận (3 điểm)

Bài 1. (1,0 điểm) Cho hai tập hợp $A = \left[ { - 1;6} \right],B = \left[ {m - 4;2m + 3} \right)$.

a) Tìm tập hợp $A \cap \mathbb{Z}$                                                           b) Tìm m để $A \cap B = \emptyset$

Bài 2. (1,0 điểm)

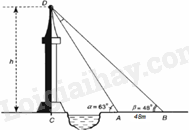
Giả sử $CD = h$ là chiều cao của một tòa tháp. Chọn hai điểm A và B trên mặt đất sao cho A, B, C thẳng hàng (xem hình vẽ). Ta đo được $AB = 48m,\widehat {CAD} = \alpha  = {63^0},\widehat {CBD} = \beta  = {48^0}$. Tính chiều cao h của tòa tháp (kết quả làm tròn đến một chữ số thập phân).

Bài 3. (1,0 điểm) Cho tam giác ABC có độ dài ba cạnh thỏa mãn $B{C^4} - A{B^4} - A{C^4} = 0$. Chứng minh rằng tam giác ABC có ba góc nhọn.

-------- Hết --------

Lời giải chi tiết

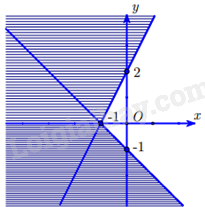
Câu 7: Miền nghiệm của một hệ bất phương trình là miền không bị gạch chéo (tính cả bờ) như hình dưới. Điểm nào sau đây nằm trong miền nghiệm của hệ bất phương trình trên?

Phương pháp

Sử dụng kiến thức: Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó. Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

Lời giải

Trong các điểm trên, chỉ có điểm $\left( {1;1} \right)$ thuộc miền không bị gạch chéo trong mặt phẳng tọa độ.

Vậy điểm có tọa độ $\left( {1;1} \right)$ nằm trong miền nghiệm của hệ bất phương trình

Đáp án D

Câu 8: Trong các hệ bất phương trình dưới đây, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?

Phương pháp

Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y

Lời giải

Hệ bất phương trình bậc nhất hai ẩn là $\left\{ \begin{array}{l}x + y \ge 0\\x - y + 5 < 0\end{array} \right.$

Đáp án B

Câu 9: Hệ bất phương trình $\left\{ \begin{array}{l}x + y > 0\\2x + 5y < 0\end{array} \right.$ có tập nghiệm là S. Khẳng định nào sau đây đúng?

Phương pháp

Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung của các bất phương trình trong hệ được gọi là một nghiệm của hệ bất phương trình đó.

Lời giải

Với $x = 1;y = \frac{1}{2}$ thay vào hệ bất phương trình $\left\{ \begin{array}{l}x + y > 0\\2x + 5y < 0\end{array} \right.$ ta có: $\left\{ \begin{array}{l}1 + \frac{1}{2} = \frac{3}{2} > 0\\2.1 + 5.\frac{1}{2} = \frac{9}{2} < 0\left( {VL} \right)\end{array} \right.$ nên $\left( {1;\frac{1}{2}} \right)\not  \in S$

Với $x = 1;y = 1$ thay vào hệ bất phương trình $\left\{ \begin{array}{l}x + y > 0\\2x + 5y < 0\end{array} \right.$ ta có: $\left\{ \begin{array}{l}1 + 1 = 2 > 0\\2.1 + 5.1 = 7 < 0\left( {VL} \right)\end{array} \right.$ nên $\left( {1;1} \right)\not  \in S$

Với $x = 1;y = \frac{{ - 1}}{2}$ thay vào hệ bất phương trình $\left\{ \begin{array}{l}x + y > 0\\2x + 5y < 0\end{array} \right.$ ta có: $\left\{ \begin{array}{l}1 - \frac{1}{2} = \frac{1}{2} > 0\\2.1 - 5.\frac{1}{2} = \frac{{ - 1}}{2} < 0\end{array} \right.$ nên $\left( {1;\frac{{ - 1}}{2}} \right) \in S$

Với $x =  - 1;y =  - 1$ thay vào hệ bất phương trình $\left\{ \begin{array}{l}x + y > 0\\2x + 5y < 0\end{array} \right.$ ta có: $\left\{ \begin{array}{l} - 1 - 1 > 0\left( {VL} \right)\\ - 2.1 - 5.1 =  - 7 < 0\end{array} \right.$ nên $\left( { - 1; - 1} \right)\not  \in S$

Đáp án C

Câu 10: Miền nghiệm của bất phương trình $- x + y > 1$ là:

A. Nửa mặt phẳng không kể bờ $d: - x + y = 1$ chứa điểm O (0; 0)

B. Nửa mặt phẳng bờ $d: - x + y = 1$ chứa điểm O (0; 0)

C. Nửa mặt phẳng bờ $d: - x + y = 1$ không chứa điểm O (0; 0)

D. Nửa mặt phẳng không kể bờ $d: - x + y = 1$ không chứa điểm O (0; 0)

Phương pháp

Biểu diễn miền nghiệm của bất phương trình $ax + by + c > 0$ như sau:

Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng $d:ax + by + c = 0$

Bước 2: Lấy một điểm $\left( {{x_0};{y_0}} \right)$ không thuộc d. Tính $a{x_0} + b{y_0} + c$

Bước 3: Kết luận: + Nếu $a{x_0} + b{y_0} + c < 0$ thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) không chứa điểm $\left( {{x_0};{y_0}} \right)$

+ Nếu $a{x_0} + b{y_0} + c > 0$ thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) chứa điểm $\left( {{x_0};{y_0}} \right)$

Lời giải

Ta thấy điểm O (0; 0) không thuộc đường thẳng $d: - x + y = 1$ và $0 + 0 < 1$ nên điểm O không thuộc miền nghiệm của bất phương trình $- x + y > 1$ . Vậy miền nghiệm của bất phương trình $- x + y > 1$ là mặt phẳng không kể bờ $d: - x + y = 1$ không chứa điểm O (0; 0)

Đáp án D

Câu 11: Trong các bất phương trình sau, bất phương trình nào không là bất phương trình bậc nhất hai ẩn?

Phương pháp

Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng

$ax + by + c > 0,ax + by + c \ge 0,ax + by + c < 0,ax + by + c \le 0$

Trong đó a, b, c là những số cho trước, a, b không đồng thời bằng 0 và x, y là các ẩn.

Lời giải

Bất phương trình ${x^2} + 2x - y > 0$ không là bất phương trình bậc nhất hai ẩn vì có chứa ${x^2}$

Đáp án B

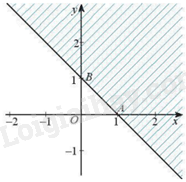
Câu 12: Cho bất phương trình có miền nghiệm là phần không bị gạch chéo (không tính bờ) như hình dưới. Điểm nào sau đây nằm trong miền nghiệm của bất phương trình trên?

Phương pháp

Trong mặt phẳng tọa độ, tập hợp các tọa độ là nghiệm của bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của bất phương trình đó.

Lời giải

Trong các điểm ở trên, chỉ có điểm $\left( {0;0} \right)$ thuộc miền không bị gạch chéo. Do đó, điểm $\left( {0;0} \right)$ nằm trong miền nghiệm của bất phương trình trong hình.

Đáp án A

Câu 13: Với ${0^0} \le \alpha  \le {180^0}$ thì:

Phương pháp

Với ${0^0} \le \alpha  \le {180^0}$ thì $\sin \left( {{{180}^0} - \alpha } \right) = \sin \alpha$

Lời giải

Với ${0^0} \le \alpha  \le {180^0}$ thì $\sin \left( {{{180}^0} - \alpha } \right) = \sin \alpha$

Đáp án A

Câu 14: Nếu $\alpha$ là góc nhọn thì:

Phương pháp

Nếu $\alpha$ là góc nhọn thì $\sin \alpha  > 0$, $\cos \alpha  > 0$

Lời giải

Nếu $\alpha$ là góc nhọn thì $\sin \alpha  > 0$, $\cos \alpha  > 0$

Đáp án C

Câu 15: Với $\alpha  \ne {90^0}$, thì:

Phương pháp

Nếu $\alpha  \ne {90^0}$ thì $\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}$

Lời giải

Nếu $\alpha  \ne {90^0}$ thì $\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}$

Đáp án A

Câu 16: Giá trị của biểu thức $A = \sin {30^0} + \cos {60^0}$ là:

Phương pháp

$\sin {30^0} = \frac{1}{2},\cos {60^0} = \frac{1}{2}$

Lời giải

$A = \sin {30^0} + \cos {60^0} = \frac{1}{2} + \frac{1}{2} = 1$

Đáp án D

Câu 17: Cho tam giác ABC có $AB = c,BC = a,AC = b$. Khi đó:

Phương pháp

Định lý côsin: Cho tam giác ABC có $AB = c,BC = a,AC = b$ thì ${a^2} = {b^2} + {c^2} - 2bc\cos A$

Lời giải  

Cho tam giác ABC có $AB = c,BC = a,AC = b$ thì theo định lí côsin ta có: ${a^2} = {b^2} + {c^2} - 2bc\cos A$

Đáp án A

Câu 18: Cho tam giác ABC có $AC = 40cm,\widehat B = {45^0}$. Bán kính của đường tròn ngoại tiếp tam giác ABC là:

Phương pháp

Định lí sin: Cho tam giác ABC có $AB = c,BC = a,AC = b$ và bán kính đường tròn ngoại tiếp tam giác là R. Khi đó, $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$

Lời giải

Áp dụng định lí sin vào tam giác ABC ta có: $R = \frac{{CA}}{{2\sin B}} = \frac{{40}}{{2\sin {{45}^0}}} = 20\sqrt 2 \left( {cm} \right)$

Đáp án D

Câu 19: Cho tam giác ABC có $AB = 5cm,BC = 6cm,\widehat B = {45^0}.$ Diện tích tam giác ABC là:

Phương pháp

Cho tam giác ABC có $AB = c,BC = a,AC = b$ thì diện tích S của tam giác ABC là: $S = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B$

Lời giải

Diện tích tam giác ABC là: $S = \frac{1}{2}AB.BC.\sin B = \frac{1}{2}.5.6.\sin {45^0} = \frac{{15\sqrt 2 }}{2}\left( {c{m^2}} \right)$

Đáp án B

Câu 20: Cho tam giác ABC có $AB = c,BC = a,AC = b$, $p = \frac{{a + b + c}}{2}$. Diện tích S của tam giác ABC là:

A. $S = p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)$

B. $S = \frac{1}{2}p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)$

C. $S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

D. $S = \frac{1}{2}\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

Phương pháp

Cho tam giác ABC có $AB = c,BC = a,AC = b$, $p = \frac{{a + b + c}}{2}$ thì diện tích S của tam giác ABC là: $S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

Lời giải

Tam giác ABC có $AB = c,BC = a,AC = b$, $p = \frac{{a + b + c}}{2}$ thì diện tích S của tam giác ABC là:

$S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

Đáp án C

Câu 21: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. 2020 là số chia hết cho 3

B. $\pi  > 3,15$

C. Tam giác có hai góc bằng nhau là tam giác đều

D. Tam giác có hai góc bằng ${45^0}$ là tam giác vuông cân 

Phương pháp

Một khẳng định đúng gọi là mệnh đề đúng, khẳng định sai gọi là mệnh đề sai.

Lời giải

Mệnh đề đúng là: Tam giác có hai góc bằng ${45^0}$ là tam giác vuông cân.

Đáp án D

Câu 22: Cho mệnh đề: “Nghiệm của phương trình ${x^2} - 10 = 0$ là số vô tỉ”. Mệnh đề phủ định của mệnh đề trên là:

A. “Nghiệm của phương trình ${x^2} - 10 = 0$ không là số vô tỉ”

B. “Nghiệm của phương trình ${x^2} - 10 = 0$ là không số hữu tỉ”

C.  “Phương trình ${x^2} - 10 = 0$ vô nghiệm”

D. “Nghiệm của phương trình ${x^2} - 10 = 0$ không là số nguyên”

Phương pháp

Mỗi mệnh đề P có mệnh đề phủ định, kí hiệu $\overline P$. Mệnh đề P và mệnh đề phủ định $\overline P$ của nó có tính đúng sai trái ngược nhau. Nghĩa là P đúng thì $\overline P$ sai, khi P sai thì $\overline P$ đúng.

Lời giải

Mệnh đề phủ định của mệnh đề trên là: Nghiệm của phương trình ${x^2} - 10 = 0$ không là số vô tỉ.

Đáp án A

Câu 23: Cho số tự nhiên n. Xét mệnh đề: “Nếu n chia hết cho 16 thì n chia hết cho 4”. Mệnh đề đảo của mệnh đề đó là:

A. Nếu n chia hết cho 16 thì n không chia hết cho 4

B. Nếu n chia hết cho 4 thì n chia hết cho 16

C. Nếu n chia hết cho 4 thì n không chia hết cho 16

D. Nếu n không chia hết cho 16 thì n không chia hết cho 4

Phương pháp

Mệnh đề đảo của mệnh đề $P \Rightarrow Q$ (hay “Nếu P thì Q”) là $Q \Rightarrow P$ (hay “Nếu Q thì P”)

Lời giải

Mệnh đề đảo của mệnh đề trên là: Nếu n chia hết cho 4 thì n chia hết cho 16

Đáp án B

Câu 24: Tập hợp $A = \left\{ {x \in \mathbb{R}|x < 2} \right\}$ được biểu diễn trên trục số là:

Phương pháp

Tập hợp $\left\{ {x \in \mathbb{R}|x < a} \right\}$ kí hiệu là khoảng $\left( { - \infty ;a} \right)$ được biểu diễn trên trục số là:

Lời giải

Tập hợp $A = \left\{ {x \in \mathbb{R}|x < 2} \right\}$ được biểu diễn trên trục số là:

Đáp án A

Câu 25: Cho các tập hợp $A = \left\{ {1;\;2;\;3} \right\}$, $B = \left\{ {2;\;3;\;4} \right\}$, $C = \left\{ {1;2;3;4} \right\}$. Chọn khẳng định đúng.

Phương pháp

Tập hợp gồm những phần tử thuộc tập hợp A hoặc thuộc tập hợp B được gọi là hợp của A và B, kí hiệu $A \cup B$.

Tập hợp gồm những phần tử vừa thuộc A vừa thuộc B được gọi là giao của A và B, kí hiệu là $A \cap B$.

Tập hợp gồm những phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu $A\backslash B$.

Lời giải

Ta có: $A \cap B = \left\{ {2;3} \right\},A \cup B = \left\{ {1;2;3;4} \right\}$. Vậy $A \cup B = C$

Đáp án C

Câu 26: Chọn đáp án đúng:

Phương pháp

Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập con của tập hợp B, và viết là $A \subset B$

Lời giải

Các khẳng định đúng là: $\left( {2;5} \right) \subset \left[ {2;5} \right]$, $\left( {2;5} \right] \subset \left[ {2;5} \right]$, $\left[ {2;5} \right) \subset \left[ {2;5} \right]$

Đáp án D

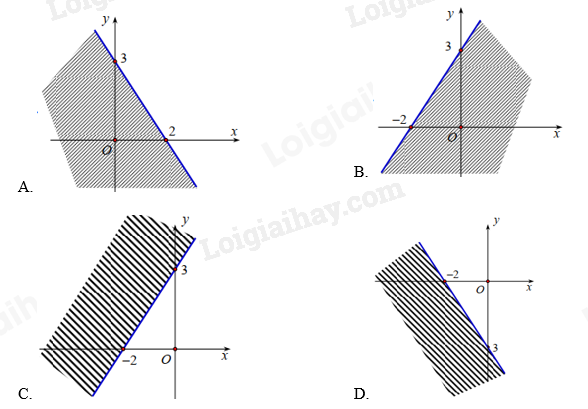
Câu 27: Cho bất phương trình: $6x + 4y - 3 > 9$. Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng tọa độ là:

Phương pháp

Biểu diễn miền nghiệm của bất phương trình $ax + by + c > 0$ như sau:

Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng $d:ax + by + c = 0$

Bước 2: Lấy một điểm $\left( {{x_0};{y_0}} \right)$ không thuộc d. Tính $a{x_0} + b{y_0} + c$

Bước 3: Kết luận: + Nếu $a{x_0} + b{y_0} + c < 0$ thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) không chứa điểm $\left( {{x_0};{y_0}} \right)$

+ Nếu $a{x_0} + b{y_0} + c > 0$ thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) chứa điểm $\left( {{x_0};{y_0}} \right)$

Lời giải

Ta có: $6x + 4y - 3 > 9 \Leftrightarrow 6x + 4y - 12 > 0 \Leftrightarrow 3x + 2y - 6 > 0$

Ta thấy điểm O (0; 0) không thuộc đường thẳng $3x + 2y - 6 = 0$ và $3.0 + 2.0 - 6 < 0$ nên miền nghiệm của bất phương trình $6x + 4y - 3 > 9$ là nửa mặt phẳng (không kể bờ d) không chứa điểm O.

Đáp án A

Câu 28: Miền nghiệm của bất phương trình $3x - 2y + 6 < 0$ là:

Phương pháp

Biểu diễn miền nghiệm của bất phương trình $ax + by + c < 0$ như sau:

Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng $d:ax + by + c = 0$

Bước 2: Lấy một điểm $\left( {{x_0};{y_0}} \right)$ không thuộc d. Tính $a{x_0} + b{y_0} + c$

Bước 3: Kết luận: + Nếu $a{x_0} + b{y_0} + c < 0$ thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) chứa điểm $\left( {{x_0};{y_0}} \right)$

+ Nếu $a{x_0} + b{y_0} + c > 0$ thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) không chứa điểm $\left( {{x_0};{y_0}} \right)$

Lời giải

Nhận thấy, điểm O (0; 0) không thuộc đường thẳng $d:3x - 2y + 6 = 0$ và $3.0 - 2.0 + 6 > 0$ nên miền nghiệm của phương trình $3x - 2y + 6 < 0$ là nửa mặt phẳng bờ là đường thẳng d (không tính bờ) không chứa điểm O.

Đáp án B

Câu 29: Cho hình vẽ sau:

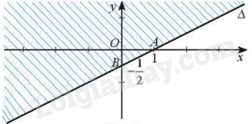
Miền không gạch chéo (không kể đường thẳng $\Delta$) là miền nghiệm của bất phương trình nào dưới đây:

Phương pháp

Biểu diễn miền nghiệm của bất phương trình $ax + by + c > 0$ như sau:

Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng $d:ax + by + c = 0$

Bước 2: Lấy một điểm $\left( {{x_0};{y_0}} \right)$ không thuộc d. Tính $a{x_0} + b{y_0} + c$

Bước 3: Kết luận: + Nếu $a{x_0} + b{y_0} + c < 0$ thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) không chứa điểm $\left( {{x_0};{y_0}} \right)$

+ Nếu $a{x_0} + b{y_0} + c > 0$ thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ d) chứa điểm $\left( {{x_0};{y_0}} \right)$

Lời giải

Đường thẳng $\Delta$ có phương trình là: $x - 2y - 1 = 0$

Ta thấy điểm O (0; 0) không thuộc đường thẳng $\Delta$, $0 - 2.0 - 1 < 0$ và điểm O không thuộc miền nghiệm của bất phương trình nên bất phương trình cần tìm là $x - 2y - 1 > 0$.

Đáp án D

Câu 30: Cho hệ bất phương trình $\left\{ \begin{array}{l}x - 2y \ge  - 2\\7x - 4y \le 16\\2x + y \ge  - 4\end{array} \right.$. Giá trị nhỏ nhất của biểu thức $F\left( {x;y} \right) = 3x - y$ với (x; y) thỏa mãn hệ bất phương trình trên là:

Phương pháp

Để tìm giá trị nhỏ nhất của biểu thức F ta làm như sau:

Bước 1: Xác định miền nghiệm của hệ bất phương trình trên, xác định các đỉnh của đa giác.

Bước 2: Tính giá trị biểu thức F tại các đỉnh của đa giác đó.

Bước 3: So sánh các giá trị thu được của F, giá trị nhỏ nhất của F là giá trị cần tìm.

Lời giải

Vẽ ba đường thẳng ${d_1}:x - 2y =  - 2,{d_2}:7x - 4y = 16,{d_3}:2x + y =  - 4$ và biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ Oxy ta được:

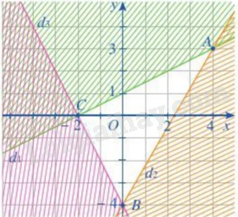
Miền nghiệm của hệ bất phương trình là miền tam giác ABC (kể cả các cạnh) với tọa độ các đỉnh $A\left( {4;3} \right),B\left( {0; - 4} \right),C\left( { - 2;0} \right)$.

Tại $A\left( {4;3} \right)$ ta có: $F = 3.4 - 3 = 9$

Tại $B\left( {0; - 4} \right)$ ta có: $F = 3.0 + 4 = 4$

Tại $C\left( { - 2;0} \right)$ ta có: $F = 3.\left( { - 2} \right) - 0 =  - 6$

Vậy giá trị nhỏ nhất của F là $- 6$ tại $x =  - 2;y = 0$

Đáp án A

Câu 31: Cho tam giác ABC. Khẳng định nào sau đây đúng?

Phương pháp

Áp dụng công thức: $\sin \alpha  = \sin \left( {{{180}^0} - \alpha } \right)$

Lời giải

Tam giác ABC có: $\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat A = {180^0} - \left( {\widehat B + \widehat C} \right)$

Ta có: $\sin A = \sin \left[ {{{180}^0} - \left( {B + C} \right)} \right] = \sin \left( {B + C} \right)$

Đáp án A

Câu 32: Cho góc $\alpha \left( {{0^0} < \alpha  < {{180}^0},\alpha  \ne {{90}^0}} \right)$ thỏa mãn $\tan \alpha  = 2$. Giá trị của biểu thức $P = \frac{{2\sin \alpha  - 3\cos \alpha }}{{3\sin \alpha  + 2\cos \alpha }}$ là:

Phương pháp

Sử dụng kiến thức $\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}$

Lời giải

$P = \frac{{2\sin \alpha  - 3\cos \alpha }}{{3\sin \alpha  + 2\cos \alpha }} = \frac{{2\frac{{\sin \alpha }}{{\cos \alpha }} - 3}}{{3\frac{{\sin \alpha }}{{\cos \alpha }} + 2}} = \frac{{2\tan \alpha  - 3}}{{3\tan \alpha  + 2}} = \frac{{2.2 - 3}}{{3.2 + 2}} = \frac{1}{8}$

Đáp án D

Câu 33: Cho tam giác ABC có $AB = 6cm,AC = 5cm,BC = 8cm$. Số đo góc A là (làm tròn đến hàng phần trăm)

Phương pháp

Định lí Côsin: Cho tam giác ABC có $AB = c,BC = a,AC = b$ thì ${a^2} = {b^2} + {c^2} - 2bc\cos A$

Lời giải

Áp dụng định lí Côsin vào tam giác ABC ta có: $B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A$

$\Rightarrow {8^2} = {6^2} + {5^2} - 2.5.6.\cos A \Rightarrow \cos A = \frac{{ - 1}}{{20}} \Rightarrow \widehat A \approx 92,{87^0}$

Đáp án C

Câu 34: Cho tam giác ABC có $AB = 13cm,BC = 14cm,AC = 15cm$. Bán kính đường tròn ngoại tiếp tam giác ABC là:

Phương pháp

Cho tam giác ABC có $AB = c,BC = a,AC = b$, p là nửa chu vi tam giác và R là bán kính đường tròn ngoài tiếp tam giác thì diện tích tam giác ABC là: $S = \frac{{abc}}{{4R}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

Lời giải

Nửa chu vi tam giác ABC là: $p = \frac{{13 + 14 + 15}}{2} = 21\left( {cm} \right)$

Diện tích tam giác ABC là: $S = \sqrt {21\left( {21 - 14} \right)\left( {21 - 15} \right)\left( {21 - 13} \right)}  = \sqrt {21.7.8.6}  = 84\left( {c{m^2}} \right)$

Bán kính đường tròn ngoại tiếp tam giác ABC là: $\frac{{AB.AC.BC}}{{4.S}} = \frac{{13.14.15}}{{4.84}} = \frac{{65}}{8}\left( {cm} \right)$

Đáp án B

Câu 35: Cho tam giác ABC có diện tích bằng $10\sqrt 3 c{m^2}$ và chu vi của tam giác bằng 20cm. Bán kính đường tròn nội tiếp r của tam giác trên là:

Phương pháp

Cho tam giác ABC có bán kính đường tròn nội tiếp là r, nửa chu vi tam giác là p thì diện tích của tam giác là $S = pr$

Lời giải

Nửa chu vi tam giác ABC là: $\frac{{20}}{2} = 10\left( {cm} \right)$. Ta có: $S = pr \Rightarrow r = \frac{S}{p} = \frac{{10\sqrt 3 }}{{10}} = \sqrt 3 \left( {cm} \right)$

Đáp án B

Phần tự luận (3 điểm)

Bài 1. (1,0 điểm) Cho hai tập hợp $A = \left[ { - 1;6} \right],B = \left[ {m - 4;2m + 3} \right)$.

a) Tìm tập hợp $A \cap \mathbb{Z}$

b) Tìm m để $A \cap B = \emptyset$

Phương pháp

Tập hợp gồm những phần tử vừa thuộc A vừa thuộc B được gọi là giao của A và B, kí hiệu là $A \cap B$.

Lời giải

a) $A \cap \mathbb{Z} = \left\{ { - 1;0;1;2;3;4;5;6} \right\}$.

b) Ta có: $A \cap B = \emptyset  \Leftrightarrow \left[ \begin{array}{l}2m + 3 \le  - 1\\m - 4 > 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \le  - 2\\m > 10\end{array} \right.$.

Bài 2. (1,0 điểm)

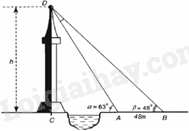
Giả sử $CD = h$ là chiều cao của một tòa tháp. Chọn hai điểm A và B trên mặt đất sao cho A, B, C thẳng hàng (xem hình vẽ). Ta đo được $AB = 48m,\widehat {CAD} = \alpha  = {63^0},\widehat {CBD} = \beta  = {48^0}$. Tính chiều cao h của tòa tháp (kết quả làm tròn đến một chữ số thập phân).

Phương pháp

Định lí sin: Cho tam giác ABC có $AB = c,BC = a,AC = b$ và bán kính đường tròn ngoại tiếp tam giác là R. Khi đó, $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$

Lời giải

Vì góc DAC là góc ngoài tại đỉnh A của tam giác DAB nên $\widehat {ADB} = \alpha  - \beta  = {15^0}$

Áp dụng định lí sin vào tam giác ADB ta có:

$\frac{{AD}}{{\sin \beta }} = \frac{{AB}}{{\sin \widehat {ADB}}} \Rightarrow AD = \frac{{48.\sin {{48}^0}}}{{\sin {{15}^0}}}\left( m \right)$

Tam giác CDA vuông tại C nên $DC = AD.\sin \alpha  \Rightarrow h = \frac{{48.\sin {{48}^0}}}{{\sin {{15}^0}}}.\sin {63^0} \approx 122,8\left( m \right)$

Bài 3. (1,0 điểm) Cho tam giác ABC có độ dài ba cạnh thỏa mãn $B{C^4} - A{B^4} - A{C^4} = 0$. Chứng minh rằng tam giác ABC có ba góc nhọn.

Phương pháp

Định lý cosin: Cho tam giác ABC có $AB = c,BC = a,AC = b$ thì ${a^2} = {b^2} + {c^2} - 2bc\cos A$

Lời giải

Ta có: $B{C^4} - A{B^4} - A{C^4} = 0$ nên $B{C^4} > A{C^4},B{C^4} > A{B^4} \Rightarrow BC > AC,BC > AB$, do đó, góc A là góc lớn nhất.

Lại có: $B{C^4} - A{B^4} - A{C^4} = 0 \Rightarrow B{C^4} = A{B^4} + A{C^4} < A{B^2}.B{C^2} + A{C^2}.B{C^2} \Rightarrow B{C^2} < A{B^2} + A{C^2}$

Do đó, $\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} > 0$. Do đó, góc A nhọn.

Vậy tam giác ABC có ba góc nhọn.