Phương pháp giải:

Hàm số \(y = f\left( x \right)\)  đồng biến trên \(\left( {a;\;b} \right) \Leftrightarrow f'\left( x \right) \ge 0\;\;\forall x \in \left( {a;\;b} \right).\)

Lời giải chi tiết:

Ta có: \(y = {x^4} - m{x^2} + 1\)\( \Rightarrow y' = 4{x^3} - 2mx.\)

Hàm số đã cho đồng biến trên \(\left( {2;\,\,3} \right)\) \( \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {2;\,\,3} \right)\)

\(\begin{array}{l} \Leftrightarrow 4{x^3} - 2mx \ge 0\,\,\forall x \in \left( {2;\,\,3} \right)\\ \Leftrightarrow 2x\left( {2{x^2} - m} \right) \ge \,0\,\,\forall x \in \left( {2;\,\,3} \right)\\ \Leftrightarrow 2{x^2} - m \ge 0\,\,\,\forall x \in \left( {2;\,\,3} \right)\\ \Leftrightarrow m \le 2{x^2}\,\,\forall x \in \left( {2;\,\,3} \right)\\ \Leftrightarrow m \le \mathop {Min}\limits_{\left( {2;\,\,3} \right)} 2{x^2}.\end{array}\)

Xét hàm số \(y = 2{x^2}\) trên \(\left( {2;\,\,3} \right)\) ta có: \(y' = 4x \Rightarrow y' = 0\, \Leftrightarrow x = 0 \notin \left( {2;\,\,3} \right)\)

Ta có bảng xét dấu:

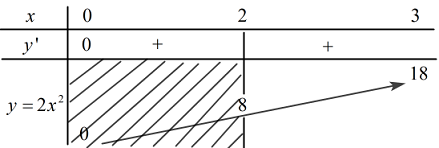
\( \Rightarrow m \le 8\)

Lại có: \(m \in {\mathbb{Z}^ + } \Rightarrow m \in \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7;\,\,8} \right\}.\)

Chọn A.