Lời giải chi tiết:

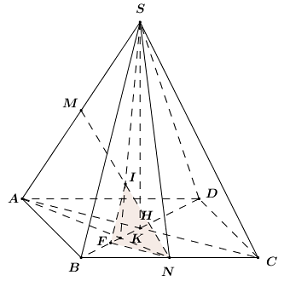
Gọi \(AC \cap BD = \left\{ H \right\} \Rightarrow SH \bot \left( {ABCD} \right).\)

Ta có: \(\left\{ \begin{array}{l}AC \bot BD\,\,\left( {gt} \right)\\AC \bot SH\,\,\left( {SH \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow AC \bot \left( {SBD} \right)\)

Gọi F là trung điểm của BH \( \Rightarrow NF\parallel AC\) (Do \(NF\) là đường trung bình của tam giác \(BCH\)).

Mà \(AC \bot \left( {SBD} \right)\) \( \Rightarrow NF \bot \left( {SBD} \right).\)

Trong mặt phẳng \(\left( {ABCD} \right)\) gọi \(AN \cap BD = \left\{ K \right\}\)

Trong mặt phẳng \(\left( {SAN} \right)\) gọi \(SK \cap MN = \left\{ I \right\}\)

\( \Rightarrow I = MN \cap \left( {SBD} \right)\).

\( \Rightarrow \angle \left( {MN;\left( {SBD} \right)} \right) = \angle \left( {NI;\left( {SBD} \right)} \right)\).

Ta có: \(FI\) là hình chiếu của \(MI\) lên \(\left( {SBD} \right)\) \( \Rightarrow \angle \left( {NI;\left( {SBD} \right)} \right) = \angle \left( {NI;FI} \right) = \angle NIF\).

Xét tam giác \(ABC\) có \(K\) là giao điểm của hai đường trung tuyến \(AN\) và \(BH\) nên \(K\) là trọng tâm của tam giác \(ABC\).

Áp dụng định lí Menelaus trong tam giác \(AMN\), cát tuyến \(SIK\) có:

\(\dfrac{{SM}}{{SA}}.\dfrac{{KA}}{{KN}}.\dfrac{{IN}}{{IM}} = 1\) \( \Leftrightarrow \dfrac{1}{2}.2.\dfrac{{IN}}{{IM}} = 1 \Leftrightarrow \dfrac{{IN}}{{IM}} = 1\) \( \Rightarrow IM = IN\) \( \Rightarrow I\) là trung điểm của \(MN\).

Ta có: \(NF = \dfrac{{HC}}{2} = \dfrac{{AC}}{4} = \dfrac{{a\sqrt 2 }}{4}\)(Tính chất đường trung bình của tam giác).

Tam giác \(SBC\) đều cạnh \(a\) nên \(SN = \dfrac{{a\sqrt 3 }}{2}.\)

Tam giác \(ABN\) vuông tại \(B\) nên áp dụng định lí Pytago ta có:

\(A{N^2} = A{B^2} + B{N^2} = {a^2} + {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{5{a^2}}}{4}.\)

Tam giác \(SAN\) có trung tuyến \(MN\)  nên:

\(\begin{array}{l}M{N^2} = \dfrac{{A{N^2} + S{N^2}}}{2} - \dfrac{{S{A^2}}}{4} = \dfrac{{\dfrac{{3{a^2}}}{4} + \dfrac{{5{a^2}}}{4}}}{2} - \dfrac{{{a^2}}}{4} = \dfrac{{3{a^2}}}{4}.\\ \Rightarrow MN = \dfrac{{a\sqrt 3 }}{2}\end{array}\)

\( \Rightarrow NI = \dfrac{{MN}}{2} = \dfrac{{a\sqrt 3 }}{4}.\)

Vì \(FN \bot \left( {SBD} \right) \Rightarrow FN \bot FI \Rightarrow \Delta FNI\) vuông tại \(F\).

\(\begin{array}{l} \Rightarrow \sin \angle FIN = \dfrac{{NF}}{{NI}} = \dfrac{{a\sqrt 2 }}{4}:\dfrac{{a\sqrt 3 }}{4} = \dfrac{{\sqrt 2 }}{{\sqrt 3 }}\\ \Rightarrow \cos \angle FIN = \sqrt {1 - {{\sin }^2}\angle FIN}  = \dfrac{{\sqrt 3 }}{3}.\end{array}\)

Chọn D.