Câu hỏi
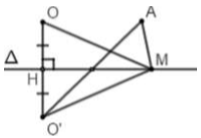
Cho \(M \in \Delta :2x - y + 1 = 0\) và hai điểm \(O\left( {0;0} \right);\,A\left( {2;1} \right)\). Tìm \(M\) để \(OM + MA\) nhỏ nhất
- A \(M\left( { - 6;13} \right)\)
- B \(M\left( {\frac{6}{{25}};\frac{{13}}{{25}}} \right)\)
- C \(M\left( {\frac{{ - 6}}{{25}};\frac{{13}}{{25}}} \right)\)
- D \(M\left( {13; - 6} \right)\)
Phương pháp giải:
Bước 1: Chứng minh \(O,A\) nằm cùng phía so với \(\Delta \)
Bước 2: Tìm \(O'\) đối xứng \(O\) qua \(\Delta \)
Bước 3: Nhận xét để \(OM + MA\) nhỏ nhất thì \(O'AM\) thẳng hàng và tìm \(M = OA' \cap \Delta \)
Lời giải chi tiết:
\(\Delta \left( O \right).\Delta \left( A \right) = \left( {2.0 - 0 + 1} \right).\left( {2.2 - 1 + 1} \right) = 1.4 > 0\)
Suy ra \(O,A\) cùng phía so với \(\Delta \)
\(d\left\{ \begin{array}{l}qua\,O\left( {0;0} \right)\\ \bot \Delta \end{array} \right. \Rightarrow d:x + 2y = 0\)\( \Rightarrow H = d \cap \Delta \Rightarrow H\left( {\frac{{ - 2}}{5};\frac{1}{5}} \right)\)
\(H\) là trung điểm \(OO' \Rightarrow \left\{ \begin{array}{l}{x_{O'}} = \frac{{ - 2}}{5}.2 - 0 = \frac{{ - 4}}{5}\\{y_{O'}} = \frac{1}{5}.2 - 0 = \frac{2}{5}\end{array} \right. \Rightarrow O'\left( {\frac{{ - 4}}{5};\frac{2}{5}} \right)\)
\(\left( {OM + MA} \right)\min = \left( {O'M + MA} \right)\min \)
\( \Rightarrow O'MA\) thẳng hàng \( \Leftrightarrow O'A \cap \Delta = M\)
\(\begin{array}{l}O'A\left\{ \begin{array}{l}qua\,\,A\left( {2;1} \right)\\VTPT\,\overrightarrow n \bot \overrightarrow {O'A} = \left( {\frac{{14}}{5};\frac{3}{5}} \right)\end{array} \right.\\ \Rightarrow 3\left( {x - 2} \right) - 14\left( {y - 1} \right) = 0 \Leftrightarrow 3x - 14y + 8 = 0\end{array}\)
\(M = O'A \cap \Delta \Rightarrow M\left\{ \begin{array}{l}3x - 14y + 8 = 0\\2x - y + 1 = 0\end{array} \right. \Rightarrow M\left( {\frac{{ - 6}}{{25}};\frac{{13}}{{25}}} \right)\)
Chọn C.