Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 Bài 2. Hai đường thẳng vuông góc
Bài 2. Hai đường thẳng vuông góc
Câu hỏi 1 trang 93 SGK Hình học 11
Cho tứ diện đều ABCD có H là trung điểm của cạnh AB. Hãy tính góc giữa các cặp vecto sau đây:...
Đề bài
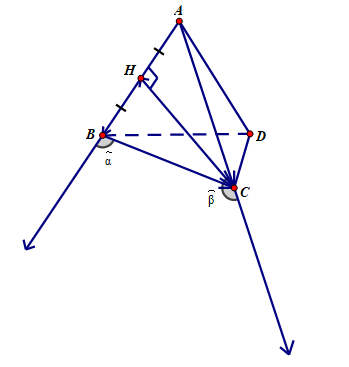
Cho tứ diện đều \(ABCD\) có \(H\) là trung điểm của cạnh \(AB\). Hãy tính góc giữa các cặp vecto sau đây:
a) \(\overrightarrow {AB}\) và \(\overrightarrow {BC}\)
b) \(\overrightarrow {CH}\) và \(\overrightarrow {AC}\)
Video hướng dẫn giải
Lời giải chi tiết
Tứ diện \(ABCD\) đều có các mặt là tam giác đều.
a) Góc giữa \(\overrightarrow {AB}\) và \(\overrightarrow {BC}\) là góc \(\alpha \) và \(\alpha = {180^0} - {60^0} = {120^0}\)
b) Góc giữa \(\overrightarrow {CH}\) và \(\overrightarrow {AC}\) là góc \(\beta \)
\(H\) là trung điểm cạnh \(AB\) của tam giác đều \(ABC\) nên \(CH\) vừa là trung tuyến vừa là đường cao nên \(CH ⊥ AB\)
Xét tam giác vuông \(ACH\) tại \(H\) có \(\widehat {ACH} + \widehat {CAH} = {90^0} \) \(\Rightarrow \widehat {ACH} = {90^0} - {60^0} = {30^0}\)
Nên \(\beta = {180^0} - {30^0} = {150^0}\)
Loigiaihay.com