Cách tìm giao tuyến của hai mặt phẳng - Toán 11

Tìm hai điểm chung phân biệt thuộc cả hai mặt phẳng. Nối hai điểm chung đó được giao tuyến cần tìm.

1) Cho tứ giác ABCD sao cho các cạnh đối không song song với nhau. Lấy một điểm S không thuộc mặt phẳng (ABCD). Xác định giao tuyến của:

a) Mặt phẳng (SAC) và mặt phẳng (SBD).

b) Mặt phẳng (SAB) và mặt phẳng (SCD).

c) Mặt phẳng (SAD) và mặt phẳng (SBC).

Giải:

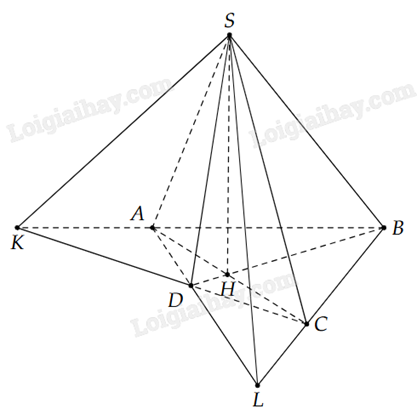
a) Gọi H là giao điểm của AC với BD.

Khi đó \(\left\{ {\begin{array}{*{20}{l}}{H \in AC}\\{H \in BD}\end{array}} \right. \Rightarrow H \in (SAC) \cap (SBD)\) (1)

Dễ thấy \(S \in (SAC) \cap (SBD)\) (2)

Từ (1) và (2) suy ra SH là giao tuyến của hai mặt phẳng (SBD) và (SAC).

b) Gọi K là giao điểm của hai đường thẳng CD và AB.

Khi đó \(\left\{ {\begin{array}{*{20}{l}}{K \in AB}\\{K \in CD}\end{array}} \right. \Rightarrow K \in (SAB) \cap (SCD)\) (3)

Dễ thấy \(S \in (SAB) \cap (SCD)\) (4)

Từ (3) và (4) suy ra SK là giao tuyến hai mặt phẳng (SAB) và (SCD).

c) Gọi L là giao điểm của hai đường thẳng AD và BC.

Khi đó \(\left\{ {\begin{array}{*{20}{l}}{L \in AD}\\{L \in BC}\end{array}} \right. \Rightarrow L \in (SAD) \cap (SBC)\) (5)

Dễ thấy \(S \in (SAD) \cap (SBC)\) (6)

Từ (5) và (6) suy ra SL là giao tuyến hai mặt phẳng (SAD) và (SBC).

2) Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm các cạnh AD, BC.

a) Tìm giao tuyến của hai mặt phẳng (IBC) và mặt phẳng (JAD).

b) Lấy điểm M thuộc cạnh AB, N thuộc cạnh AC sao cho M, N không là trung điểm. Tìm giao tuyến của mặt phẳng (IBC) và mặt phẳng (DMN).

Giải:

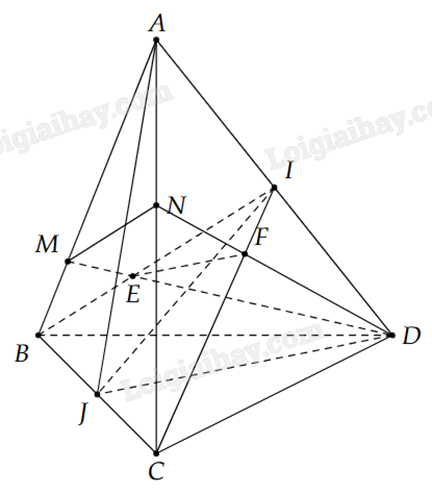
a) Do giả thiết \(I \in AD\) nên \(I \in (JAD)\).

- Suy ra \(I \in (BCI) \cap (ADI)\) (1).

- Tương tự, ta có \(J \in (BCI) \cap (JAD)\) (2).

- Từ (1) và (2) suy ra IJ là giao tuyến của hai mặt phẳng (BCI) và (JAD).

b) Gọi E là giao điểm của hai đường thẳng DM và BI.

- Khi đó \(\left\{ {\begin{array}{*{20}{l}}{E \in BI}\\{E \in DM}\end{array}} \right. \Rightarrow E \in (MND) \cap (IBC)\) (3).

- Tương tự, gọi F là giao điểm của DN và CI suy ra \(F \in (BCI) \cap (MND)\) (4).

- Từ (3) và (4) suy ra EF là giao tuyến hai mặt phẳng (BCI) và (MND).

3) Cho tứ diện ABCD. Lấy các điểm M thuộc cạnh AB, N thuộc cạnh AC sao cho MN cắt BC. Gọi I là điểm bên trong tam giác BCD. Tìm giao tuyến của

a) Mặt phẳng (MNI) và mặt phẳng (BCD).

b) Mặt phẳng (MNI) và mặt phẳng (ABD).

c) Mặt phẳng (MNI) và mặt phẳng (ACD).

Giải:

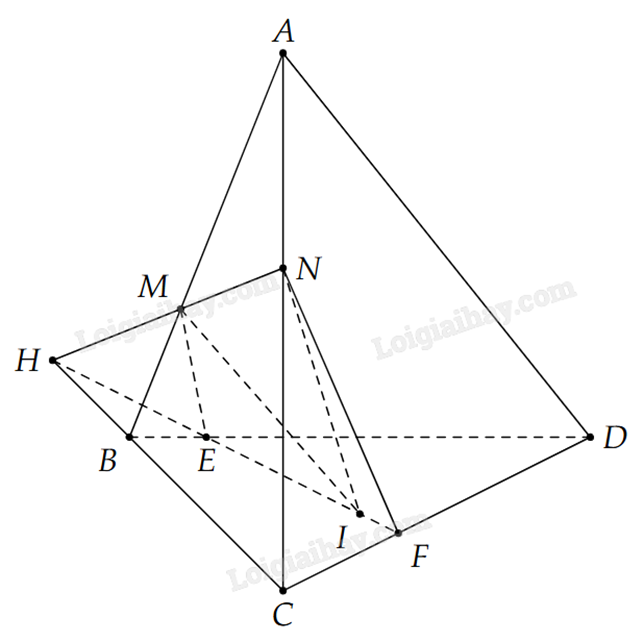
a) Gọi H là giao điểm của MN và BC.

Suy ra \(H \in (MNI) \cap (BCD)\) (1).

Do I là điểm trong \(\Delta BCD\) nên \(I \in (MNI) \cap (BCD)\) (2).

Từ (1) và (2) suy ra HI là giao tuyến của hai mặt phẳng (MNI) và (BCD).

b) Giả sử E là giao điểm của hai đường thẳng HI và BD.

Vì \(H \in MN\) và

\(\left\{ {\begin{array}{*{20}{l}}{E \in BD}\\{E \in HI}\end{array}} \right. \Rightarrow E \in (MNI) \cap (ABD)\) (3)

Mặt khác \(M \in AB\) nên \(M \in (MNI) \cap (ABD)\) (4).

Từ (3) và (4) suy ra ME là giao tuyến của hai mặt phẳng (MNI) và (ABD).

c) Gọi F là giao điểm của HI và CD.

Ta có \(\left\{ {\begin{array}{*{20}{l}}{F \in CD}\\{F \in HI}\end{array}} \right. \Rightarrow F \in (MNI) \cap (ACD)\) (5)

Và \(N \in AC\) nên \(N \in (MNI) \cap (ACD)\) (6).

Từ (5) và (6) suy ra NF là giao tuyến của hai mặt phẳng (MNI) và (ACD).