Cho hình bình hành ABCD có A(–1;–2), B(3;2), C(4;−1). Toạ độ của đỉnh D là:
A. (8; 3)
B. (3; 8)
C. (-5; 0)
D. (0; -5)
Bước 1: Tham số hóa tọa độ điểm D và xác định tọa độ vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \).
Bước 2: Áp dụng kết quả tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {DC} = \overrightarrow {AB} \) để tìm tọa độ điểm D.
Giả sử D(a; b) ta có \(\overrightarrow {DC} = (4 - a; - 1 - b)\) và \(\overrightarrow {AB} = (4;4)\).
ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}4 - a = 4\\ - 1 - b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = - 5\end{array} \right. \Rightarrow D(0; - 5)\).
Chọn D

Các bài tập cùng chuyên đề
Tìm tọa độ của \(\overrightarrow 0 \)
Trong Hình 4.33:
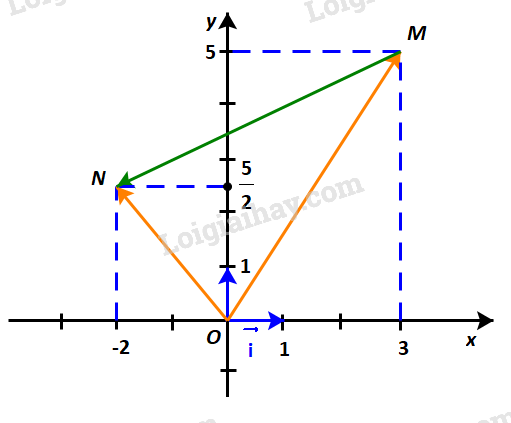
a) Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
b) Hãy biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) từ đó biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
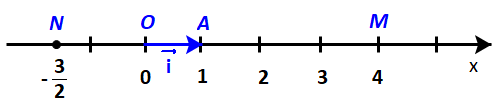
Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt \(\overrightarrow {OA} = \overrightarrow i \) (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số \( - \frac{3}{2}\). Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo vectơ \(\overrightarrow i \).
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 3), N(4; 2)
a) Tính độ dài các đoạn thẳng OM, ON, MN.
b) Chứng minh rằng tam giác OMN vuông cân.
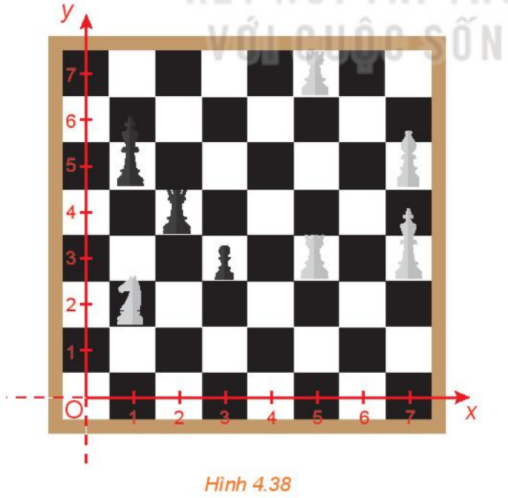
Trong hình 4.38, quân mã đang ở vị trí có tọa độ (1; 2). Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?
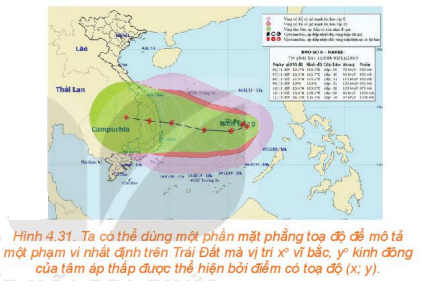
Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ. Trong khoảng thời gian đó, tâm bāo di chuyển thẳng đều từ vị trí có tọa độ (13,8; 108,3) đến vị trí có toạ độ (14,1;106,3). Dựa vào thông tin trên, liệu ta có thể dự đoán được vị trí của tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó hay không?
Cho \(E\left( {9;9} \right), F\left( {8; - 7} \right), G\left( {0; - 6} \right)\). Tìm tọa độ các vectơ \(\overrightarrow {FE} ,\overrightarrow {FG} ,\overrightarrow {EG} \).
Cho hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm tọa độ vectơ \(\overrightarrow {AB} \) theo tọa độ hai điểm A, B.
Tìm tọa độ của các vectơ sau:
a) \(\overrightarrow a = 2\overrightarrow i + 7\overrightarrow j ;\)
b) \(\overrightarrow b = - \overrightarrow i + 3\overrightarrow j ;\)
c) \(\overrightarrow c = 4\overrightarrow i ;\)
d) \(\overrightarrow d = - 9\overrightarrow j \)
Hình 1 minh hoạ hoạt động của một màn hình ra đa ở trạm kiểm soát không lưu của sân bay, đang theo dõi một máy bay hạ cánh. Máy bay xuất hiện trên màn hình ra đa bởi một điểm sáng, ký hiệu là M. Dựa trên sự thay đổi của tọa độ vecto \(\overrightarrow {OM} \), trạm kiểm soát có thể xác định được đường bay của máy bay.
Tọa độ của vecto \(\overrightarrow {OM} \) là gì?
Trong mặt phẳng tọa độ Oxy, cho điểm B(-1;0) và vecto \(\overrightarrow v = \left( {0; - 7} \right)\).
a) Biểu diễn vecto \(\overrightarrow v \) qua hai vecto \(\overrightarrow i ,\overrightarrow j \).
b) Biểu diễn vecto \(\overrightarrow {OB} \) qua hai vecto\(\overrightarrow i ,\overrightarrow j \).
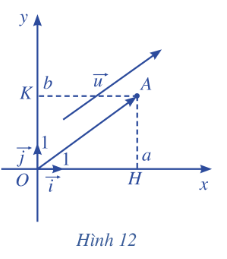
Trong mặt phẳng toạ độ Oxy, cho vectơ\(\overrightarrow u {\rm{ }} = {\rm{ }}\left( {a;{\rm{ }}b} \right)\) . Ta chọn điểm A sao cho\(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) . Xét vectơ đơn vị \(\overrightarrow i \) trên trục hoành Ox và vectơ đơn vị \(\overrightarrow j \) ở trên trục tung Oy (Hình 12).
a) Tìm hoành độ và tung độ của điểm A.
b) Biểu diễn vectơ OH qua vectơ \(\overrightarrow i \).
c) Biểu diễn vectơ OK qua vecto \(\overrightarrow j \).
d) Chứng tỏ rằng \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \).
Tìm tọa độ của các vecto \(\overrightarrow c ,\overrightarrow d \) trong Hình 11.

Trong mặt phẳng toạ độ Oxy, cho vectơ \(\overrightarrow u \) (Hình 7). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \overrightarrow u \).
Trong mặt phẳng toạ độ Oxy, cho hai điểm A, B (Hình 13).
a) Tìm hoành độ\({x_A}\) và tung độ\({y_A}\) của điểm A; hoành độ \({x_B}\) và tung độ \({y_B}\) của điểm B.
b) Tìm điểm M sao cho\(\overrightarrow {OM} {\rm{ }} = {\rm{ }}\overrightarrow {AB} \). Từ đó, tìm hoành độ a và tung độ b của vectơ \(\overrightarrow {AB} \).
c) So sánh: \({x_B} - {x_A}\) và a; \({y_B} - {y_A}\) và b.
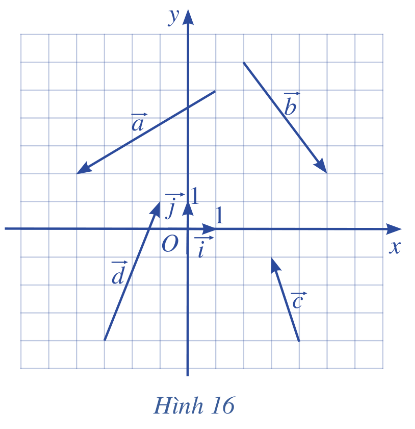
Tìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto \(\overrightarrow i , \overrightarrow j \).
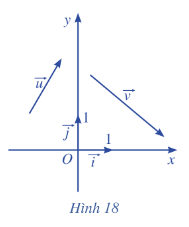
Trong mặt phẳng toạ độ Oxy (Hình 18), cho hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\) và \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\).
a) Biểu diễn các vectơ \(\overrightarrow u ,\overrightarrow v \) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \).
b) Biểu diễn các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \).
c) Tìm tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)
Tìm tọa độ của các vecto sau:
a) \(\overrightarrow a = 3\overrightarrow i \)
b) \(\overrightarrow b = - \overrightarrow j \)
c) \(\overrightarrow c = \overrightarrow i - 4\overrightarrow j \)
d) \(\overrightarrow d = 0,5\overrightarrow i + \sqrt 6 \overrightarrow j \)
Trong mặt phẳng tọa độ Oxy, cho \(A\left( {3;4} \right)\), \(B\left( {2;5} \right)\). Tọa độ của \(\overrightarrow {AB} \) là:
A. \(\left( {1; - 1} \right)\)
B. \(\left( {1;1} \right)\)
C. \(\left( { - 1;1} \right)\)
D. \(\left( { - 1; - 1} \right)\)
Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai điểm A(2;3) và B(-1;2). Tọa độ \(\overrightarrow {BA} \) là
-
A.
(-1;5)
-
B.
(-3;-1)
-
C.
(3;1)
-
D.
(1;5)
Trong mặt phẳng tọa độ Oxy, cho các điểm M(4;-3) và N(-2;0). Tọa độ của vecto \(\overrightarrow {MN} \) là
-
A.
(2;-3)
-
B.
(6;-3)
-
C.
(-6;3)
-
D.
(-2;3)
Tọa độ của vectơ \(\overrightarrow u = 5\overrightarrow j \) là:
A. \((5;0)\)
B. \((5;\overrightarrow j )\)
C. \((0;5\overrightarrow j )\)
D. \((0;5)\)
Trong mặt phẳng toạ độ Oxy, cho A(2; −5). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. (2 ; 5)
B. (2; −5)
C. (−2; −5)
D. (−2; 5)
Trong mặt phẳng toạ độ Oxy, cho A(−1; 3), B(2; −1). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. (1; -4)
B. (-3; 4)
C. (3; -4)
D. (1; -2)
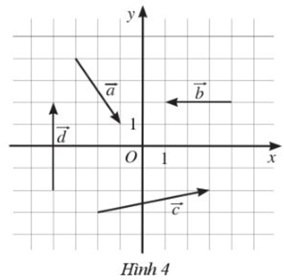
Tìm toạ độ của các vectơ trong Hình 4.
Toạ độ của vectơ \(\overrightarrow u = - 3\overrightarrow i + 2\overrightarrow j \) là:
A. \(( - 3;2)\)
B. \((2; - 3)\)
C. \(( - 3\overrightarrow i ;2\overrightarrow j )\)
D. \((3;2)\)
Trong mặt phẳng toạ độ Oxy, cho \(\overrightarrow u = ( - 2; - 4),\overrightarrow v = (2x - y;y)\). Hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng nhau nếu:
A. \(\left\{ \begin{array}{l}x = 1\\y = - 4\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = - 3\\y = - 4\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 1\\y = 4\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = - 3\\y = 4\end{array} \right.\)
Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:
a) \(\overrightarrow m = (2a + 3;b - 1)\) và \(\overrightarrow n = (1; - 2)\).
b) \(\overrightarrow u = (3a - 2;5)\)và \(\overrightarrow v = (5;2b + 1)\).
c) \(\overrightarrow x = (2a + b;2b)\) và \(\overrightarrow y = (3 + 2b;b - 3a)\).
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 4 ; 2), B(2 ; 4), C(8 ; – 2). Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.
Trong mặt phẳng toạ độ Oxy, cho tứ giác ABCD có \(A({x_A};{y_A});B({x_B};{y_B});C({x_C};{y_C});D({x_D};{y_D})\). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi \({x_A} + {x_C} = {x_B} + {x_D}\) và \({y_A} + {y_C} = {y_B} + {y_D}\).






