Đề bài

Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a, gọi O là giao điểm của AC và BD. Khoảng cách giữa hai đường thẳng AB và SD bằng

A. $\frac{{a\sqrt 6 }}{3}$ .

B. $\frac{{a\sqrt 3 }}{2}$ .

C. . $\frac{{a\sqrt 6 }}{3}$ .

D. $\frac{{a\sqrt 6 }}{2}$ .

Phương pháp giải

Gọi $M,N$ lần lượt là trung điểm của các cạnh $AB,CD$ ; $H$ là hình chiếu vuông góc của $O$ trên $SN.$

Vì $AB{\rm{//}}CD$ nên $d\left( {AB,SD} \right) = d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)$

Ta có $\left\{ \begin{array}{l}CD \bot SO\\CD \bot ON\end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH$

Khi đó $\left\{ \begin{array}{l}CD \bot OH\\OH \bot SN\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.$

Tam giác $SOD$ vuông tại $O$ nên $O{S^2} = S{D^2} - O{D^2}$

Tam giác $SON$ vuông tại $O$ nên $\frac{1}{{O{H^2}}} = \frac{1}{{O{N^2}}} + \frac{1}{{O{S^2}}} \Rightarrow OH$

Vậy $d\left( {AB,SD} \right) = 2OH$ .

Lời giải của GV Loigiaihay.com

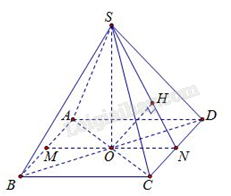
Gọi $M,N$ lần lượt là trung điểm của các cạnh $AB,CD$ ; $H$ là hình chiếu vuông góc của $O$ trên $SN.$

Vì $AB{\rm{//}}CD$ nên $d\left( {AB,SD} \right) = d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)$

Ta có $\left\{ \begin{array}{l}CD \bot SO\\CD \bot ON\end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH$

Khi đó $\left\{ \begin{array}{l}CD \bot OH\\OH \bot SN\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.$

Tam giác $SOD$ vuông tại $O$ nên $O{S^2} = S{D^2} - O{D^2} = {a^2} - {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = \frac{{{a^2}}}{2}$

Tam giác $SON$ vuông tại $O$ nên $\frac{1}{{O{H^2}}} = \frac{1}{{O{N^2}}} + \frac{1}{{O{S^2}}} = \frac{1}{{\frac{{{a^2}}}{4}}} + \frac{1}{{\frac{{{a^2}}}{2}}} = \frac{6}{{{a^2}}} \Rightarrow OH = \frac{a}{{\sqrt 6 }} = \frac{{a\sqrt 6 }}{6}$

Vậy $d\left( {AB,SD} \right) = 2OH = \frac{{a\sqrt 6 }}{3}$ .

Xem thêm : SBT Toán 11 - Kết nối tri thức

Báo lỗi/Góp ý

Các bài tập cùng chuyên đề

Cho đường thẳng a vuông góc với mặt phẳng (P) và cắt (P) tại O. Cho đường thẳng b thuộc mặt phẳng (P). Hãy tìm mối quan hệ giữa khoảng cách giữa a, b và khoảng cách từ O đến b (H.7.88).

Xem lời giải >>

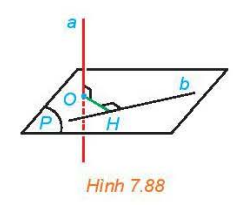
Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).

a) Mặt phẳng chứa a và a' có vuông góc với (Q) hay không?

b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không?

c) Nêu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN.

Xem lời giải >>

Một căn phòng có trần cao 3,2 m. Tỉnh khoảng cách giữa một đường thẳng $a$ trên trần nhà và đường thẳng $b$ trên sàn nhà.

Xem lời giải >>

Cho tứ diện $OABC$ có ba cạnh $OA,OB,OC$ đều bằng $a$ và vuông góc từng đôi một. Tính khoảng cách giữa hai đường thẳng:

a) $OA$ và $BC$ ;

b) $OB$ và $AC$ .

Xem lời giải >>

Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$ , $SA = SB = SC = SD = a\sqrt 2$ . Gọi $I,J$ lần lượt là trung điểm của $AB$ và $C{\rm{D}}$ .

a) Chứng minh $AB \bot \left( {SIJ} \right)$ .

b) Tính khoảng cách giữa hai đường thẳng $AB$ và $SC$ .

Xem lời giải >>

Một cây cầu dành cho người đi bộ (Hình 22) có mặt sàn cầu cách mặt đường 3,5 m, khoảng cách từ đường thẳng $a$ nằm trên tay vịn của cầu đến mặt sàn cầu là 0,8 m. Gọi $b$ là đường thẳng kẻ theo tim đường. Tính khoảng cách giữa hai đường thẳng $a$ và $b$ .

Xem lời giải >>

Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$ , $SA \bot \left( {ABCD} \right)$ và $SA = a$ . Gọi $M,N,P$ lần lượt là trung điểm của $SB,SC$ và $SD$ . Tính khoảng cách giữa $AM$ và $NP$ .

Xem lời giải >>

Cho hình lập phương $ABCD.A'B'C'D'$ có $AC' = \sqrt 3$ . Khoảng cách giữa hai đường thẳng $AB'$ và $BC'$ bằng

A. $\frac{1}{3}$ .

B. $\frac{{\sqrt 3 }}{3}$ .

C. $\frac{{\sqrt 3 }}{2}$ .

D. $\frac{1}{2}$

Xem lời giải >>

Cho hình chóp tam giác $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a,SA \bot \left( {ABC} \right)$ . Tính $d\left( {SA,BC} \right)$ .

Xem lời giải >>

Trong Hình 73, khuôn cửa phía trên và mép cánh cửa phía dưới gợi nên hình ảnh hai đường thẳng $a$ và $b$ chéo nhau, hai bản lề của cánh cửa nằm trên đường thẳng $c$ .

Quan sát Hình 73 và cho biết đường thẳng $c$ có vừa cắt, vừa vuông góc với cả hai đường thẳng $a$ và $b$ hay không.

Xem lời giải >>

Cho hình hộp chữ nhật $MNPQ.M'N'P'Q'$ có $MN = 2a,MQ = 3a,$ $MM' = 4a$ . Khoảng cách giữa hai đường thẳng $NP$ và $M'N'$ bằng:

A. $2a$ .

B. $3a$ .

C. $4a$ .

D. $5a$ .

Xem lời giải >>

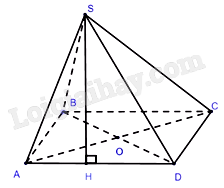
Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O, AB = a, BC = $a\sqrt 3$ , chân đường cao hình chóp là điểm H thuộc cạnh AD sao cho DH = 2AH, góc giữa SD và mặt phẳng đáy bằng $60^\circ$ . Khoảng cách giữa hai đường thẳng SB và AC bằng bao nhiêu?

Xem lời giải >>

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’. Tính khoảng cách giữa hai đường thẳng MN và B’D’.

Xem lời giải >>

Cho hình tứ diện đều ABCD có cạnh bằng $\sqrt {11}$ . Gọi I là trung điểm của cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI.

Xem lời giải >>

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, $AB = 2a,BC = a$ , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD. Tính theo a khoảng cách giữa hai đường thẳng BE và SC.

A. $\frac{{a\sqrt {30} }}{{10}}$

B. $\frac{{a\sqrt 3 }}{2}$

C. $\frac{{a\sqrt {15} }}{5}$

D. a

Xem lời giải >>

Cho hình chóp S. ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho $HA = 2HB$ . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng ${60^0}$ . Tính khoảng cách giữa hai đường thẳng SA và BC theo a.

Xem lời giải >>

Cho hình chóp đều $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $a$ , cạnh bên $SA$ bằng $a\sqrt 2$ . Khoảng cách giữa hai đường thẳng $BD$ và $SC$ là

A. $\frac{{a\sqrt 6 }}{4}$ .

B. $\frac{{a\sqrt 6 }}{3}$ .

C. $\frac{{a\sqrt 6 }}{2}$ .

D. $\frac{{a\sqrt 3 }}{2}$ .

Xem lời giải >>

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh bằng $a$ và $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$ . Khoảng cách giữa hai đường thẳng $SA$ và $BC$ bằng

A. $\frac{{a\sqrt 2 }}{2}$ .

B. $\frac{{a\sqrt 3 }}{4}$ .

C. $\frac{{a\sqrt 6 }}{2}$ .

D. $\frac{{a\sqrt 3 }}{2}$ .

Xem lời giải >>

Cho hình lăng trụ đứng ABC.A'B'C' có AB = 5, BC = 6, CA = 7. Khoảng cách giữa hai đường thẳng AA' và BC bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).

Xem lời giải >>

Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng 2, cạnh bên bằng $2\sqrt 2$ . Tính khoảng cách giữa hai đường thẳng AB và SD (kết quả làm tròn đến hàng phần mười).

Xem lời giải >>

Cho tứ diện đều ABCD có cạnh bằng 2. Khoảng cách giữa hai đường thẳng AB và CD bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?

Xem lời giải >>

Cho hình chóp S.ABCD có $SA \bot (ABCD)$ , đáy ABCD là hình chữ nhật và AD = 6. Góc giữa cạnh bên SD và mặt đáy bằng ${30^o}$ . Khoảng cách giữa hai đường thẳng AB và SD bằng bao nhiêu?

Xem lời giải >>

Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có AB = 2 cm, AC = 6 cm, $\widehat {BAC} = {150^o}$ . Khoảng cách giữa hai đường thẳng BB’ và AC bằng bao nhiêu (đơn vị: cm)?

Xem lời giải >>

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B với AB = BC = 1, AD = 2. Biết $SA \bot (ABCD)$ và SA = 1. Tính khoảng cách giữa AD và SB (tính chính xác đến hàng phần trăm).

Xem lời giải >>

Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng 2, cạnh bên bằng $2\sqrt 2$ . Tính khoảng cách giữa hai đường thẳng AB và SD (kết quả làm tròn đến hàng phần mười).

Xem lời giải >>

TẢI APP ĐỂ XEM OFFLINE