Cho hai điểm A(1; 3; 0) và B(5; 1; −2). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là
A. \(2x - y - z + 5 = 0\)
B. \(2x - y - z - 5 = 0\)
C. \(x + y + z - 3 = 0\)
D. \(3x + 2y - z - 4 = 0\)
Phương trình mặt phẳng có dạng:
\({n_1}(x - {x_0}) + {n_2}(y - {y_0}) + {n_3}(z - {z_0}) = 0\)
trong đó \(({x_0},{y_0},{z_0})\) là tọa độ của một điểm trong mặt phẳng và \(({n_1},{n_2},{n_3})\) là tọa độ của véc-tơ pháp tuyến.
Trung điểm M của đoạn AB có tọa độ:
\(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right) = \left( {\frac{{1 + 5}}{2};\frac{{3 + 1}}{2};\frac{{0 - 2}}{2}} \right) = \left( {3;2; - 1} \right)\)
Véc-tơ \(\overrightarrow {AB} \) có tọa độ:
\(\overrightarrow {AB} = ({x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A}) = (5 - 1;1 - 3; - 2 - 0) = (4; - 2; - 2)\)
Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng vuông góc với đoạn AB. Do đó, véc-tơ \(\overrightarrow {AB} \) cũng là véc-tơ pháp tuyến của mặt phẳng trung trực. Vậy, véc-tơ pháp tuyến \(\vec n\) của mặt phẳng trung trực là:
\(\vec n = (4, - 2, - 2)\)
Gọi phương trình mặt phẳng trung trực là \(4x - 2y - 2z + D = 0\). Vì mặt phẳng này đi qua trung điểm \(M(3,2, - 1)\), nên tọa độ của M phải thỏa mãn phương trình mặt phẳng này:
\(4 \cdot 3 - 2 \cdot 2 - 2 \cdot ( - 1) + D = 0\)
\(12 - 4 + 2 + D = 0\)
\(10 + D = 0 \Rightarrow D = - 10\)
Vậy, phương trình mặt phẳng trung trực của đoạn thẳng AB là:
\(4x - 2y - 2z - 10 = 0\)
\(2x - y - z - 5 = 0\)
Chọn B

Các bài tập cùng chuyên đề
Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right):x + 2 = 0\).
a) Điểm \(A\left( { - 2;1;0} \right)\) có thuộc \(\left( \alpha \right)\) hay không?
b) Hãy chỉ ra một vectơ pháp tuyến của \(\left( \alpha \right)\).
Trong không gian Oxyz, phương trình nào trong các phương trình sau là phương trình tổng quát của một mặt phẳng?
a) \({x^2} + 2{y^2} + 3{z^2} - 1 = 0\);
b) \(\frac{x}{2} - y + \frac{z}{3} + 5 = 0\);
c) \(xy + 5 = 0\).
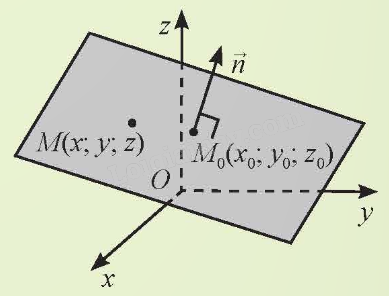
Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\).
Dựa vào HĐ4, hãy nêu phương trình của \(\left( \alpha \right)\).
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x - 2y - 3z + 1 = 0\). Một vectơ pháp tuyến của mặt phẳng (P) có tọa độ là
A. \(\left( {1;2;3} \right)\).
B. \(\left( {1; - 2;3} \right)\).
C. \(\left( {1;2; - 3} \right)\).
D. \(\left( {1; - 2; - 3} \right)\).
Trong không gian Oxyz, cho đường thẳng d: \(\left\{ \begin{array}{l}x = 1 + t\\y = - 2 + t\\z = 4 - 2t\end{array} \right.\). Viết phương trình mặt phẳng (P) chứa đường thẳng d và gốc tọa độ O.
Trong không gian Oxyz, cho điểm \(M\left( {2; - 1;3} \right)\). Gọi A, B, C lần lượt là hình chiếu vuông góc của M trên Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là
A. \(3x - 6y + 2z + 6 = 0\).
B. \(3x - 6y + 2z + 6 = 0\).
C. \(3x - 2y + 2z - 1 = 0\).
D. \(3x - 6y + 2z - 1 = 0\).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm A(1;-1;2) và có vecto pháp tuyến là \(\overrightarrow n = (1;2;3)\)
Giả sử M(x;y;z) là một điểm tùy ý thuộc mặt phẳng (P) (Hình 7)
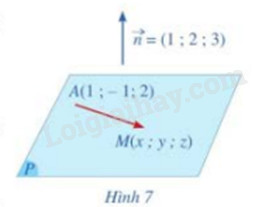
a) Tính tích vô hướng \(\overrightarrow n .\overrightarrow {AM} \) theo x, y, z
b) Tọa độ (x;y;z) của điểm M có thỏa mãn phương trình: x + 2y + 3z – 5 = 0 hay không?
Phương trình nào sau đây là phương trình tổng quát của mặt phẳng?
A. \( - {x^2} + 2y + 3z + 4 = 0\)
B. \(2x - {y^2} + z + 5 = 0\)
C. \(x + y - {z^2} + 6 = 0\)
D. \(3x - 4y - 5z + 1 = 0\)
Mặt phẳng (P): \(3x - 4y + 5z - 6 = 0\) có một vectơ pháp tuyến là:
A. \(\overrightarrow {{n_1}} = \left( {3;4;5} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {3; - 4;5} \right)\).
C. \(\overrightarrow {{n_3}} = \left( { - 3;4;5} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {3;4; - 5} \right)\).
Phương trình nào sau đây là phương trình tổng quát của mặt phẳng?
A. \(x - {y^2} - 2 = 0\).
B. \(x + {z^2} - 3 = 0\).
C. \(x - z - 4 = 0\).
D. \({x^2} + {y^2} + {z^2} - 1 = 0\).
Trong không gian Oxyz, cho điểm \(H\left( {3;2;4} \right)\).
a) Viết phương trình mặt phẳng \(\left( P \right)\) chứa điểm H và trục Oy.
b) Viết phương trình mặt phẳng \(\left( Q \right)\) đi qua điểm H và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C (với A, B, C đều không trùng với gốc tọa độ O) sao cho H là trực tâm tam giác ABC.
Cho mặt phẳng \(\left( P \right):x - 2y + z - 5 = 0\). Điểm nào dưới đây thuộc \(\left( P \right)\)?
A. \(M\left( {1;1;6} \right)\).
B. \(N\left( { - 5;0;0} \right)\).
C. \(P\left( {0,0, - 5} \right)\).
D. \(Q\left( {2; - 1;5} \right)\).
Tứ diện ABCD có các đỉnh \((A(5;1;3),B(1;6;2),C(5;0;4),D(4;0;6)\).
a) Hãy viết phương trình của các mặt phẳng \((ACD)\) và \((BCD)\).
b) Hãy viết phương trình mặt phẳng \(\left( \alpha \right)\) chứa cạnh AB và song song với cạnh CD.
Trong không gian Oxyz, mặt phẳng (P): x – 3z + 2 = 0 đi qua điểm nào sau đây?
-
A.
E(1;1;1)
-
B.
F(1;1;0)
-
C.
H(7;3;1)
-
D.
G(4;2;0)
Trong không gian Oxyz, cho mặt phẳng (P): 2x + 4y – z = 3. Vecto nào sau đây là vecto pháp tuyến của (P)?
-
A.
\(\overrightarrow {{n_1}} = (2;4; - 1)\)
-
B.
\(\overrightarrow {{n_2}} = (2; - 4;1)\)
-
C.
\(\overrightarrow {{n_3}} = ( - 2;4;1)\)
-
D.
\(\overrightarrow {{n_4}} = (2;4;1)\)
Trong không gian Oxyz, phương trình nào sau đây là phương trình tổng quát của mặt phẳng?
-
A.
\(2x + 3y + z - 1 = 0\)
-
B.
\({x^2} + y - z + 3 = 0\)
-
C.
\(x - {y^2} + 3z - 6 = 0\)
-
D.
\(x + y + {z^2} - 7 = 0\)
Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua gốc tọa độ?
-
A.
x + 20 = 0
-
B.
x – 2019 = 0
-
C.
y + 5 = 0
-
D.
2x + 5y – 8z = 0
Trong không gian Oxyz, cho mặt phẳng (P): x – 2y + z – 1 = 0. Điểm nào sau đây không thuộc mặt phẳng (P)?
-
A.
E(0;0;1)
-
B.
F(3;1;0)
-
C.
M(2;-1;3)
-
D.
N(3;2;2)
Trong không gian Oxyz, phương trình nào sau đây là phương trình tổng quát của một mặt phẳng?
-
A.
\({x^2} + 2{y^2} - 3{z^2} + 1 = 0\)
-
B.
\(\frac{1}{x} + \frac{2}{y} + \frac{3}{z} + 2 = 0\)
-
C.
\(x - y + 1 = 0\)
-
D.
\(xy + 5 = 0\)
Trong không gian Oxyz, cho mặt phẳng (P): x + y – 3z – 4 = 0. Điểm nào sau đây không thuộc mặt phẳng (P)?
-
A.
A(0;4;0)
-
B.
B(1;-6;-3)
-
C.
C(2;2;0)
-
D.
D(2;2;1)
Trong không gian Oxyz, điểm nào dưới đây thuộc mặt phẳng (P): x – 2y + 3z – 2 = 0?
-
A.
P(1;-2;1)
-
B.
M(1;-2;3)
-
C.
Q(-1;2;1)
-
D.
N(1;-2;-1)
Cho điểm A(1;2;−1) và mặt phẳng \(\left( \alpha \right)\): x – 2y + 2z + 2 = 0. Mặt phẳng \(\left( \beta \right)\) song song với mặt phẳng \(\left( \alpha \right)\) và cách A một khoảng 1 có dạng \(\left( \beta \right)\): x – by + cz + d = 0. Khi đó S = 3b – c + d bằng bao nhiêu?
Trong không gian Oxyz, cho hai điểm A(1;2;0), B(3;4;−2) và P : x – y + z − 4 = 0. Phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P ), có dạng (Q) : ax + by + cz + 2 = 0. Tính T = a + b + c.
Trong không gian Oxyz, đường thẳng d: \(\left\{ \begin{array}{l}x = - 1 + t\\y = 2 - 3t\\z = t\end{array} \right.\) và điểm A(2;3;1). Mặt phẳng (P) đi qua điểm A vuông góc với đường thẳng d có phương trình là
-
A.
2x + 3y + z + 6 = 0
-
B.
x – 3y + z + 6 = 0
-
C.
x – 3y + z – 6 = 0
-
D.
-x + 3y – z + 5 = 0
Xác định m để mặt phẳng (P): 3x – 4y + 2z + m = 0 đi qua điểm A(3;1;-2).
-
A.
m = -1
-
B.
m = 1
-
C.
m = 9
-
D.
m = -9
Trong không gian Oxyz, làm thế nào để xác định một mặt phẳng bằng phương pháp tọa độ?
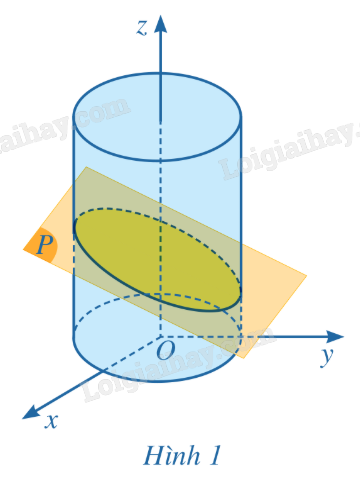
Người ta muốn sản xuất một chi tiết máy được cắt ra từ một ống trụ thép bằng gia công cơ khí chính xác (Hình 1). Để làm chi tiết máy đó, người ta cần xác định phương trình của mặt cắt trong một hệ tọa độ thích hợp và đưa những dữ liệu đó vào hệ thống máy tính điều khiển các máy gia công cơ khí kĩ thuật số. Trong không gian với hệ tọa độ Oxyz, phương trình của mặt phẳng là gì? Làm thế nào để lập được phương trình của mặt phẳng?
Trong không gian Oxyz, mặt phẳng (P) đi qua điểm M(3; -1; 4) đồng thời vuông góc với giá của vectơ $\overset{\rightarrow}{a} = \left( {1; - 1;2} \right)$ có phương trình là
-
A.
$3x - y + 4z - 12 = 0$.
-
B.
$3x - y + 4z + 12 = 0$.
-
C.
$x - y + 2z - 12 = 0$.
-
D.
$x - y + 2z + 12 = 0$.







Danh sách bình luận