Viết phương trình tham số của đường thẳng \(\Delta \), biết \(\Delta \) đi qua điểm \(C\left( {1;2; - 4} \right)\) và vuông góc với mặt phẳng (P): \(3x - y + 2z - 1 = 0\).
Sử dụng kiến thức về phương trình tham số của đường thẳng để viết phương trình tham số đường thẳng: Hệ phương trình \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\), trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
Mặt phẳng (P) có một vectơ pháp tuyến là \(\overrightarrow n \left( {3; - 1;2} \right)\).
Vì đường thẳng \(\Delta \) vuông góc với mặt phẳng (P) nên đường thẳng \(\Delta \) nhận \(\overrightarrow n \left( {3; - 1;2} \right)\) làm một vectơ chỉ phương.
Lại có, \(\Delta \) đi qua điểm \(C\left( {1;2; - 4} \right)\) nên phương trình tham số của đường thẳng \(\Delta \) là: \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 2 - t\\z = - 4 + 2t\end{array} \right.\) (t là tham số).

Các bài tập cùng chuyên đề
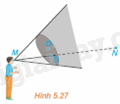
(H.5.27) Trong tình huống mở đầu hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.
a) Viết phương trình tham số của đường thẳng MN.
b) Tính tọa độ giao điểm D của đường thẳng MN với mặt phẳng Oxy.
c) Hỏi điểm D có nằm giữa hai điểm M và N hay không?
Trong không gian Oxyz, viết phương trình tham số của đường thẳng \(\Delta \) đi qua điểm \(M\left( {2; - 1;3} \right)\) và vuông góc với mặt phẳng Oyz.
Trong không gian Oxyz, viết phương trình tham số và phương trình chính tắc của đường thẳng \(\Delta \) đi qua điểm \(A\left( {2; - 1;0} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( { - 1;2;3} \right)\).
Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\) (a, b, c là các số khác 0).
a) Điểm \(M\left( {x;y;z} \right)\) thuộc \(\Delta \) khi và chỉ khi hai vectơ \(\overrightarrow {AM} \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\) và \(\overrightarrow u = \left( {a;b;c} \right)\) có mối quan hệ gì?
b) Điểm \(M\left( {x;y;z} \right)\) thuộc \(\Delta \) khi và chỉ các phân số \(\frac{{x - {x_0}}}{a};\frac{{y - {y_0}}}{b};\frac{{z - {z_0}}}{c}\) có mối quan hệ gì?
Trong không gian Oxyz, cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 + t\\y = 3t\\z = 1 + t\end{array} \right.\).
a) Hãy chỉ ra hai điểm thuộc \(\Delta \) và một vectơ chỉ phương của \(\Delta \).
b) Viết phương trình tham số của đường thẳng đi qua gốc tọa độ O(0; 0; 0) và có vectơ chỉ phương \(\overrightarrow v = \left( {1;3;1} \right)\).
Trong không gian Oxyz, cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\\z = 3 - t\end{array} \right.\). Một vectơ chỉ phương của đường thẳng d có tọa độ là
A. \(\left( {1; - 2;3} \right)\).
B. \(\left( {2;0;0} \right)\).
C. \(\left( {2;1; - 1} \right)\).
D. \(\left( {2;1;1} \right)\).
Trong không gian Oxyz, cho hai điểm \(A\left( { - 1;0; - 1} \right),B\left( {2;1;1} \right)\). Phương trình đường thẳng AB là
A. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = t\\z = 1 + 2t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = - 1 + t\\y = t\\z = - 1 + 2t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 2 + t\\y = 1 + t\\z = 1 + 2t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = - 1 + 3t\\y = t\\z = - 1 + 2t\end{array} \right.\).
Cho đường thẳng \(\Delta \) có phương trình tham số:
\(\left\{ \begin{array}{l}x = 2 + 3t\\y = 4 + 7t\\z = 5 + 8t\end{array} \right.\) (t là tham số).
Tọa độ (x; y; z) của điểm M (nằm trên \(\Delta \)) có thỏa mãn hệ phương trình \(\frac{{x - 2}}{3} = \frac{{y - 4}}{7} = \frac{{z - 5}}{8}\) hay không?
Đường thẳng đi qua điểm A(3; 2; 5) nhận \(\overrightarrow u = \left( { - 2;8; - 7} \right)\) làm vectơ chỉ phương có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = - 2 + 3t\\y = 8 + 2t\\z = - 7 + 5t\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = 3 - 2t\\y = 2 - 8t\\z = 5 - 7t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 3 - 2t\\y = 2 + 8t\\z = 5 + 7t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = 3 - 2t\\y = 2 + 8t\\z = 5 - 7t\end{array} \right.\)
Cho đường thẳng \(\Delta \) có phương trình tham số \(\left\{ \begin{array}{l}x = 1 - t\\y = 3 + 2t\\z = - 1 + 3t\end{array} \right.\)(t là tham số).
a) Chỉ ra tọa độ hai điểm thuộc đường thẳng \(\Delta \).
b) Điểm nào trong các điểm \(C\left( {6; - 7; - 16} \right),D\left( { - 3;11; - 11} \right)\) thuộc đường thẳng \(\Delta \)?
Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\) với \({a_1}\), \({a_2}\), \({a_3}\) đều khác 0. Lấy điểm \(M\left( {x;y;z} \right)\) bất kì thuộc \(d\). So sánh các biểu thức \(\frac{{x - {x_0}}}{{{a_1}}}\); \(\frac{{y - {y_0}}}{{{a_2}}}\); \(\frac{{z - {z_0}}}{{{a_3}}}.\)
Viết phương trình tham số của đường thẳng \(a\) trong mỗi trường hợp sau:
a) Đường thẳng \(a\) đi qua điểm \(M\left( {0; - 2; - 3} \right)\) và có vectơ chỉ phương \(\vec a = \left( {1; - 5;0} \right)\)
b) Đường thẳng \(a\) đi qua hai điểm \(A\left( {0;0;2} \right)\) và \(B\left( {3; - 2;5} \right)\).
Cho đường thẳng \(d\) có phương trình chính tắc \(\frac{{x - 3}}{1} = \frac{{y + 3}}{3} = \frac{{z - 2}}{7}\).
a) Tìm một vectơ chỉ phương của \(d\) và một điểm trên \(d\).
b) Viết phương trình tham số của \(d\).
Viết phương trình tham số của đường thẳng \(d\) đi qua điểm \(A\left( {1;0;1} \right)\) và song song với đường thẳng \(d':\frac{{x + 1}}{3} = \frac{{y - 1}}{2} = \frac{{z - 1}}{4}\).
Đường thẳng đi qua điểm \(A\left( { - 8; - 3;7} \right)\) và nhận \(\overrightarrow u = \left( {3; - 4;2} \right)\) làm vectơ chỉ phương có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = 3 - 8t\\y = - 4 - 3t\\z = 2 + 7t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = - 8 + 3t\\y = - 3 + 4t\\z = 7 + 2t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 3 + 8t\\y = - 4 + 3t\\z = 2 + 7t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = - 8 + 3t\\y = - 3 - 4t\\z = 7 + 2t\end{array} \right.\).
Đường thẳng \(\Delta \) có phương trình chính tắc là: \(\frac{{x + 1}}{{ - 7}} = \frac{{y + 3}}{{ - 8}} = \frac{{z - 2}}{1}\). Phương trình tham số của \(\Delta \) là:
A. \(\left\{ \begin{array}{l}x = 1 - 7t\\y = 3 - 8t\\z = - 2 + t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = - 1 + 7t\\y = - 3 + 8t\\z = 2 + t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = - 1 - 7t\\y = 3 - 8t\\z = 2 + t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = - 1 - 7t\\y = - 3 - 8t\\z = 2 + t\end{array} \right.\).
Đường thẳng đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và vuông góc với mặt phẳng \(\left( {Oxy} \right)\) có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = {x_0}\\y = {y_0}\\z = t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = t\\y = {y_0}\\z = {z_0}\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = {x_0}\\y = t\\z = {z_0}\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = {x_0} + t\\y = {y_0} + t\\z = {z_0} + t\end{array} \right.\).
Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = 7 + 5t\\y = 3 + 11t\\z = 9 - 6t\end{array} \right.\).
Tìm một điểm trên \(d\) và một vectơ chỉ phương của \(d\).
Lập phương trình tham số của đường thẳng \(d\) trong mỗi trường hợp sau:
a) \(d\) đi qua điểm \(A\left( {1; - 5;0} \right)\) và có vectơ chỉ phương \(\overrightarrow a = \left( {2;0;7} \right)\);
b) \(d\) đi qua hai điểm \(M\left( {3; - 1; - 1} \right),N\left( {5;1;2} \right)\).
Cho đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{3 - y}}{{ - 1}} = z + 1\). Trong các phương trình sau, phương trình nào là phương trình tham số của \(d\)?
A. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 - t\\z = - 1\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 3 + t\\z = - 1 + t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + t\\z = - 1 + t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 + t\\z = - 2 + t\end{array} \right.\).
Phương trình nào dưới đây là phương trình của đường thẳng đi qua \(A\left( {2;3;0} \right)\) và vuông góc với mặt phẳng \(\left( P \right):x + 3y - z + 5 = 0\)?
A. \(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 3t\\z = 1 - t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 1 + t\\y = 3t\\z = 1 - t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + 3t\\z = 1 - t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + 3t\\z = 1 + t\end{array} \right.\).
Trong không gian Oxyz, cho đường thẳng \(d\) qua \({M_0}({x_0};{y_0};{z_0})\) có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Phương trình tham số của đường thẳng là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Giả sử \({a_1},{a_2},{a_3}\) đều khác 0. Hãy tính các tỉ số \(\frac{{x - {x_0}}}{{{a_1}}},\frac{{y - {y_0}}}{{{a_2}}},\frac{{z - {z_0}}}{{{a_3}}}\) theo \(t\) và so sánh các tỉ số này.
Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\).
a) Viết phương trình tham số của \(d\).
b) Tìm điểm \(M\) thuộc \(d\) biết \(OM = 7\).
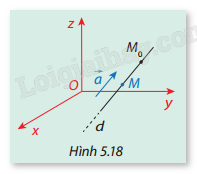
Trong không gian \(Oxyz\), cho đường thẳng \(d\) qua điểm \({M_0}({x_0};{y_0};{z_0})\), có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Giả sử \(M(x;y;z)\) là một điểm bất kỳ trên \(d\)(Hình 5.18). Ta biết \(\overrightarrow {{M_0}M} \) cùng phương với \(\vec a\) nên tồn tại số thực \(t\) sao cho \(\overrightarrow {{M_0}M} = t\vec a\).
a) Hãy tính tọa độ điểm \(M\) theo \({x_0},{y_0},{z_0},{a_1},{a_2},{a_3},t\).
b) Bạn An cho rằng điều kiện cần và đủ để \(M(x;y;z) \in d\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\)
Bạn An phát biểu đúng hay không? Vì sao?
Trong không gian Oxyz, phương trình đường thẳng đi qua M(1;2;3) và song song với trục Oy có phương trình tham số là
-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2}\\{z = 3}\end{array}} \right.\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2}\\{z = 3}\end{array}} \right.\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 2 + t}\\{z = 3}\end{array}} \right.\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 2}\\{z = 3 + t}\end{array}} \right.\)
Trong không gian Oxyz, trục Ox có phương trình tham số là
-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 0}\\{z = t}\end{array}} \right.\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = 0}\\{z = 0}\end{array}} \right.\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = t}\\{z = t}\end{array}} \right.\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = 1}\\{z = 1}\end{array}} \right.\)
Trong không gian với hệ tọa độ Oxyz, viết phương trình tham số của đường thẳng đi qua điểm M(1;2;3) và song song với giao tuyến của hai mặt phẳng (P): 3x + y – 3 = 0, (Q): 2x + y + z – 3 = 0.
-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 + 3t}\\{z = 3 + t}\end{array}} \right.\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 - 3t}\\{z = 3 - t}\end{array}} \right.\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 - 3t}\\{z = 3 + t}\end{array}} \right.\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x = 1 - t}\\{y = 2 - 3t}\\{z = 3 + t}\end{array}} \right.\)
Trong không gian với hệ tọa độ Oxyz, giao điểm của hai đường thẳng d: \(\left\{ {\begin{array}{*{20}{c}}{x = - 3 + 2t}\\{y = - 2 + 3t}\\{z = 6 + 4t}\end{array}} \right.\) và d’: \(\left\{ {\begin{array}{*{20}{c}}{x = 5 + t'}\\{y = - 1 - 4t'}\\{z = 20 + t'}\end{array}} \right.\) có tọa độ là
-
A.
(5;-1;20)
-
B.
(-3;-2;6)
-
C.
(3;7;18)
-
D.
(3;-2;1)
Viết phương trình tham số của đường thẳng:
a) Đi qua hai điểm \(A(1;0; - 3)\) và \(B( - 3;1;0)\).
b) Đi qua điểm \(M(2;3; - 5)\) và song song với đường thẳng \(\Delta \): \(\left\{ {\begin{array}{*{20}{l}}{x = - 2 + 2t}\\{y = 3 - 4t}\\{z = - 5t\quad (t \in \mathbb{R})}\end{array}} \right.\)
Cho đường thẳng \(\Delta \) đi qua điểm \(M(2;0; - 1)\) và có vectơ chỉ phương \(\vec a = (2; - 3;1)\). Phương trình tham số của đường thẳng \(\Delta \) là:
A. \(\left\{ {\begin{array}{*{20}{l}}{x = - 2 + 4t}\\{y = - 6t}\\{z = 1 + 2t}\end{array}} \right.\quad (t \in \mathbb{R})\)
B. \(\left\{ {\begin{array}{*{20}{l}}{x = 2 + 2t}\\{y = - 3}\\{z = - 1 + t}\end{array}} \right.\quad (t \in \mathbb{R})\)
C. \(\left\{ {\begin{array}{*{20}{l}}{x = 2 + 2t}\\{y = - 3t}\\{z = - 1 + t}\end{array}} \right.\quad (t \in \mathbb{R})\)
D. \(\left\{ {\begin{array}{*{20}{l}}{x = 2 + 2t}\\{y = - 3t}\\{z = 1 + t}\end{array}} \right.\quad (t \in \mathbb{R})\)






