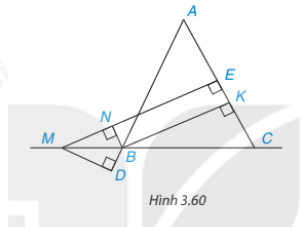
Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E và K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N, D lần lượt là chân đường vuông góc hạ từ B xuống ME và từ M xuống AB. (H.3.60)
Chứng minh rằng:
a) Tứ giác BKEN là hình chữ nhật
b) BK và NE cùng bằng hiệu khoảng cách từ M đến AC và AB (dù M thay đổi trên đường thẳng MC miễn là B nằm giữa M và C)
a) Tứ giác BKEN có ba góc bằng 90o
b) Chứng minh ΔMBD = ΔMBN (cạnh huyền – góc nhọn)
Suy ra MD = MN
Lại có: BK = NE = ME – MN suy ra BK = NE = ME − MD.
a) Xét tứ giác BKEN có: \(\widehat {BKE} = \widehat {KEN} = \widehat {ENB} = {90^o}\)
Suy ra tứ giác BKEN là hình chữ nhật
b) D là chân đường vuông góc hạ từ M đến AB
Ta có BN // AC (do BKNE là hình chữ nhật) suy ra \(\widehat {MBN} = \widehat {BCA}\)(hai góc đồng vị)
\(\widehat {MB{\rm{D}}} = \widehat {ABC}\)(đối đỉnh)
Mà \(\widehat {ABC} = \widehat {BCA}\)(tam giác ABC cân tại A) suy ra \(\widehat {MBN} = \widehat {MB{\rm{D}}}\)
Xét tam giác vuông MBD và MBN ta có:
BM chung
\(\widehat {MB{\rm{D}}} = \widehat{MBN} \)
Suy ra ΔMBD = ΔMBN (cạnh huyền – góc nhọn)
Suy ra MD = MN
Lại có: BK = NE = ME – MN suy ra BK = NE = ME − MD

Các bài tập cùng chuyên đề
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
a) Hỏi tứ giác MPAN là hình gì?
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
Cho tam giác ABC vuông tại A có M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh tứ giác ABCD là hình chữ nhật và \(AM = \dfrac{1}{2}BC\).
Cho hình chữ nhật ABCD có điểm E nằm trên cạnh CD sao cho \(\widehat {A{\rm{E}}B} = {78^o};\widehat {EBC} = {39^o}\). Tính số đo của \(\widehat {BEC}\) và \(\widehat {E{\rm{A}}B}\).
Hình chữ nhật ABCD có O là giao điểm của hai đường chéo AC và BD. Hãy tìm độ dài thích hợp cho các ô \(?\) trong bảng dưới đây:
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
a) Hỏi tứ giác MPAN là hình gì?
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
Cho tam giác ABC cân tại A, AH là đường cao. Gọi M, N lần lượt là trung điểm của AB, AC. Gọi D, E lần lượt là điểm sao cho M là trung điểm của HD, N là trung điểm của HE.
a) Chứng minh AHBD, AHCE, BCED là những hình chữ nhật.
b) Tại sao giao điểm của BE và CD là trung điểm của AH?
c) Giải thích tại sao \(DH = HE,BE = CD\).
Cho \(\Delta ABC\) vuông tại A (AB < AC) có I là trung điểm BC. Gọi K là điểm đối xứng của A qua I.
a) Chứng minh ABKC là hình chữ nhật.
b) Gọi D, E lần lượt là trung điểm AB và BK. Chứng minh rằng ID \( \bot \)AB và \(DI = \frac{1}{2}BK\)
c) Qua I vẽ đường thẳng vuông góc với BI tại I và cắt BA, BK lần lượt tại F và G. Gọi H, J lần lượt là trung điểm của FI và IG. Chứng minh rằng DH // EJ.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC và M là trung điểm của BC. Chứng minh rằng:
a) \(EF = AH\)
b) \(AM \bot EF\)
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
-
A.
M là hình chiếu của A trên BC
-
B.
M là trung điểm của BC
-
C.
M trùng với B
-
D.
Đáp án khác