Bài 1 trang 88 SGK Hình học 10
Xác đinh độ dài các trục, tọa độ tiêu điểm , tọa độ các đỉnh và vẽ các elip có phương trình sau:
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Video hướng dẫn giải
Xác định độ dài các trục, tọa độ tiêu điểm, tọa độ các đỉnh và vẽ các elip có phương trình sau:
LG a
\(\frac{x^{2}}{25} + \frac{y^{2}}{9}= 1.\)
Phương pháp giải:
Cho phương trình ellip: \(\left( E \right):\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{b^2} = 1.\)
Khi đó:
+) Độ dài trục lớn là: \(2a\) và độ dài trục nhỏ là \(2b.\)
+) Tọa độ các đỉnh là: \({A_1}\left( { - a;\;0} \right),\;{A_2}\left( {a;\;0} \right),\;{B_1}\left( { - b;\;0} \right),\)\(\;{B_2}\left( {b;\;0} \right).\)
+) Tọa độ tiêu điểm: \({F_1}\left( { - c;\;0} \right),\;{F_2}\left( {c;\;0} \right)\) với \(c^2=a^2-b^2.\)
Lời giải chi tiết:
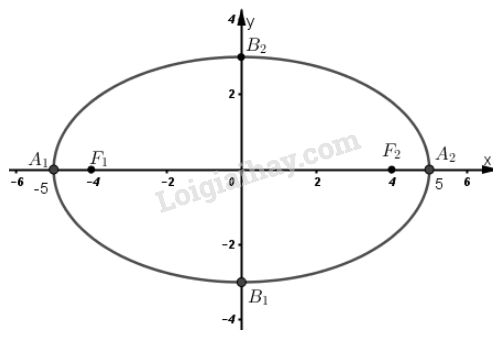
Ta có: \(a^2= 25 \Rightarrow a = 5\) độ dài trục lớn \(2a = 10\)
\( b^2= 9 \Rightarrow b = 3\) độ dài trục nhỏ \(2b = 6\)
\(c^2= a^2– b^2= 25 - 9 = 16 \Rightarrow c = 4\)
Vậy hai tiêu điểm là : \(F_1(-4 ; 0)\) và \(F_2(4 ; 0)\)
Tọa độ các đỉnh \(A_1(-5; 0), A_2(5; 0), B_1(0; -3), B_2(0; 3)\).
LG b
\(4x^2+ 9y^2= 1.\)
Lời giải chi tiết:
\(4x^2+ 9y^2= 1\Leftrightarrow \dfrac{x^{2}}{\dfrac{1}{4}} + \dfrac{y^{2}}{\dfrac{1}{9}} = 1\)
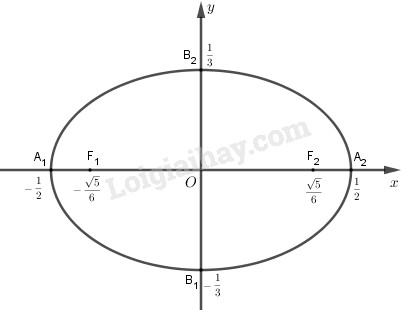
\(a^2 =\dfrac{1}{4}\Rightarrow a = \dfrac{1}{2}\) \(\Rightarrow\) độ dài trục lớn \(2a = 1\)
\(b^2= \dfrac{1}{9}\Rightarrow b = \dfrac{1}{3}\) \(\Rightarrow\) độ dài trục nhỏ \(2b = \dfrac{2}{3}\)
\(c^2= a^2– b^2= \dfrac{1}{4}- \dfrac{1}{9} = \dfrac{5}{36}\) \(\Rightarrow c = \dfrac{\sqrt{5}}{6}\)
\(F_1(-\dfrac{\sqrt{5}}{6} ; 0)\) và \(F_2(\dfrac{\sqrt{5}}{6} ; 0)\)
\(A_1(-\dfrac{1}{2}; 0), A_2(\dfrac{1}{2}; 0)\), \(B_1(0; -\dfrac{1}{3} ), B_2(0; \dfrac{1}{3} )\).
LG c
\(4x^2+ 9y^2= 36.\)
Lời giải chi tiết:
Chia \(2\) vế của phương trình cho \(36\) ta được :
\(\dfrac{x^{2}}{9}+ \dfrac{y^{2}}{4}= 1\)
Ta có:
\(\begin{array}{l}
{a^2} = 9 \Rightarrow a = 3\\
{b^2} = 4 \Rightarrow b = 2\\
{c^2} = {a^2} - {b^2} = 5 \Rightarrow c = \sqrt 5
\end{array}\)
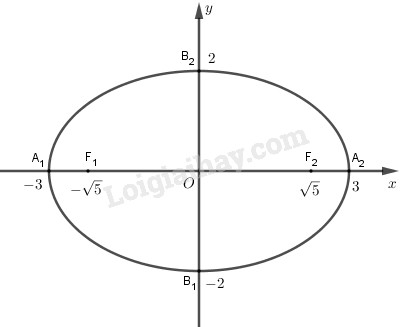
+) Độ dài trục lớn \(2a = 6\)
+) Độ dài trục nhỏ \( 2b = 4\).
+) Tiêu điểm \(F_1(-\sqrt5 ; 0)\) và \(F_2(\sqrt5 ; 0)\)
+) Các đỉnh \(A_1(-3; 0), A_2(3; 0), B_1(0; -2), B_2(0; 2)\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2 trang 88 SGK Hình học 10
- Bài 3 trang 88 SGK Hình học 10
- Bài 4 trang 88 SGK Hình học 10
- Giải bài 5 trang 88 SGK Hình học 10
- Câu hỏi 4 trang 87 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
