Đề thi học kì 2 Toán 11 - Đề số 8
Câu 1: Với b,c là hai số thực dương tùy ý thỏa mãn log5b≥log5c, khẳng định nào dưới đây là đúng? A. b≥c. B. b≤c. C. b>c. D. b<c.
Đề bài
Câu 1 : Với b,c là hai số thực dương tùy ý thỏa mãn log5b≥log5c, khẳng định nào dưới đây là đúng?
-
A.
b≥c.
-
B.
b≤c.
-
C.
b>c.
-
D.
b<c.
Câu 2 : Đạo hàm của hàm số y=2x là:
-
A.
y′=2xln2
-
B.
y′=2x
-
C.
y′=2xln2
-
D.
y′=x2x−1
Câu 3 : Nghiệm của phương trình 2x=3 là
-
A.
x=log23.
-
B.
x=log32.
-
C.
x=3.
-
D.
x=2.
Câu 4 : Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a,AA′⊥(ABCD) và AA′=3a. Thể tích của khối lăng trụ đã cho bằng
-
A.
a3.
-
B.
3a3.
-
C.
2a3.
-
D.
3a34⋅
Câu 5 : Cho hình lập phương ABCD⋅A′B′C′D′ có cạnh bằng a (tham khảo hình vẽ).
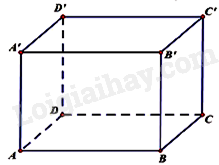
Gọi φ là góc giữa hai mặt phẳng (BDA′) và (ABCD). Giá trị của sinφ bằng
-
A.
√63.
-
B.
√34.
-
C.
√33.
-
D.
√64.
Câu 6 : Hệ số góc tiếp tuyến của đồ thị hàm số y=2x2−2 tại điểm có hoành độ x0=2là:
-
A.
4
-
B.
8
-
C.
6
-
D.
-4
Câu 7 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,SA vuông góc với đáy, SA=a. Khoảng cách giữa hai đường thẳng SB và CD là
-
A.
a.
-
B.
2a.
-
C.
a√2.
-
D.
a√3.
Câu 8 : Có hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,6. Xác suất để có ít nhất một người bắn trúng là:
-
A.
0,95.
-
B.
0,92.
-
C.
0,48.
-
D.
0.96.
Câu 9 : Tính đạo hàm của hàm số sau y=−3x+4x−2.
-
A.
y′=2(x−2)2.
-
B.
y′=−11(x−2)2.
-
C.
y′=−5(x−2)2.
-
D.
y′=10(x−2)2.
Câu 10 : Cho hình chóp S.ABC,SA vuông góc với đáy, J là hình chiếu của A trên BC. Khẳng định nào sau đây là đúng?
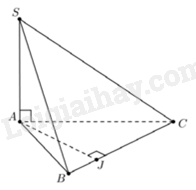
-
A.
BC⊥(SAJ).
-
B.
AJ⊥SC.
-
C.
BC⊥(SAC).
-
D.
BC⊥(SAB)
Câu 11 : Có ba chiếc hộp: hộp I có 4 bi đỏ và 5 bi xanh, hộp II có 3 bi đỏ và 2 bi đen, hộp III có 5 bi đỏ và 3 bi vàng. Lấy ngẫu nhiên ra một hộp rồi lấy một viên bi từ hộp đó. Xác suất để viên bi lấy được màu đỏ bằng
-
A.
6011080.
-
B.
611.
-
C.
16.
-
D.
61360.
Câu 12 : Tập nghiệm của bất phương trình log7(5x−2)>log7(6−3x) là
-
A.
S=(1;+∞).
-
B.
S=(1;2).
-
C.
S=(2;+∞).
-
D.
S=(25;1).
Câu 13 : Tập nghiệm của bất phương trình 5x+2<(125)−x là
-
A.
(2;+∞).
-
B.
(−∞;1).
-
C.
(−∞;2).
-
D.
(1;+∞).
Câu 14 : Hàm số y=(1+x)√1−xcó đạo hàm y′=ax+b2√1−x. Tính a+b.
-
A.
−2.
-
B.
2.
-
C.
−3.
-
D.
1
Câu 15 : Tìm tất cả các giá trị của tham số m để phương trình 9x−2.6x+m.4x=0 có hai nghiệm trái dấu.
-
A.
0<m<1.
-
B.
m<−1 hoặc m>1.
-
C.
m≤1.
-
D.
m<0
Câu 16 : Hai xạ thủ tham gia thi đấu bắn súng, mỗi người bắn vào bia của mình một viên đạn một cách độc lập với nhau. Gọi A và B lần lượt là các biến cố "Người thứ nhất bắn trúng bia"; "Người thứ hai bắn trúng bia". Khẳng định nào sau đây đúng?
-
A.
Hai biến cố A và B bằng nhau.
-
B.
Hai biến cố A và B đối nhau.
-
C.
Hai biến cố A và B độc lập với nhau.
-
D.
Hai biến cố A và B không độc lập với nhau.
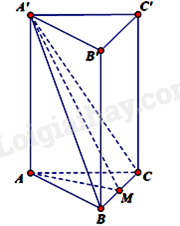
Câu 17 : Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng nhau. Gọi α là góc tạo bởi hai đường thẳng B'C và AB. Tính cosin của góc α.
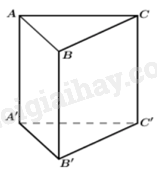
-
A.
cosα=√36
-
B.
cosα=√24
-
C.
cosα=−√34
-
D.
cosα=√22
Câu 18 : Cho (cos2x−tan3x)′=asin2x+bcos23x. Tính S=a−b?
-
A.
S=−5
-
B.
S=−1
-
C.
S=1
-
D.
S=5
Câu 19 : Một chất điểm chuyển động trong 20 giây đầu tiên có phương trình s(t)=112t4−t3+6t2+10t, tròng đó t>0tính bằng giây và S(t) tính bằng mét (m). Hỏi tại thời điểm t=3s thì vận tốc của vật bằng bao nhiêu?
-
A.
18m/s.
-
B.
28m/s .
-
C.
13m/s.
-
D.
17m/s.
Câu 20 : Câu lạc bộ cờ vua của một trường THPT có 20 thành viên ở ba khối, trong đó khối 10 có 3 nam và 2 nữ, khối 11 có 4 nam và 4 nữ, khối 12 có 5 nam và 2 nữ. Giáo viên chọn ngẫu nhiên một thành viên của câu lạc bộ để tham gia thi đấu giao hữu. Xét các biến cố sau:
A : "Thành viên được chọn là học sinh khối 11";
B : "Thành viên được chọn là học sinh nam".
Khi đó biến cố A∪B là
-
A.
"Thành viên được chọn là học sinh khối 11 và là học sinh nam".
-
B.
"Thành viên được chọn là học sinh khối 11 và không là học sinh nam".
-
C.
"Thành viên được chọn là học sinh khối 11 hoặc là học sinh nam".
-
D.
"Thành viên được chọn không là học sinh khối 11 hoặc là học sinh nam".
Câu 21 : Cho khối lăng trụ ABC⋅A′B′C′ có thể tích là 4. Khối chóp A′⋅ABC có thể tích bằng
-
A.
4.
-
B.
12.
-
C.
43.
-
D.
83.
Câu 22 : Cho hàm số y=x3−3x2+2 có đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 3 có dạng ax+by−25=0. Khi đó, tổng a+b bằng:
-
A.
8.
-
B.
−10.
-
C.
−8.
-
D.
10.
Câu 23 : Một hộp chứa 12 chiếc thẻ có kích thước như nhau, trong đó có 5 chiếc thẻ màu xanh được đánh số từ 1 đến 5; có 4 chiếc thẻ màu đỏ được đánh số từ 1 đến 4 và 3 chiếc thẻ màu vàng được đánh số từ 1 đến 3. Lấy ngẫu nhiên 2 chiếc thẻ từ hộp, tính xác suất để 2 chiếc thẻ được lấy vừa khác màu vừa khác số.
-
A.
2966.
-
B.
3766.
-
C.
833.
-
D.
1433.
Câu 24 : Cho A,B là hai biến cố độc lập. Biết P(A)=14,P(A∩B)=19. Tính P(B)
-
A.
736.
-
B.
15.
-
C.
49.
-
D.
536.
Câu 25 : Cho hình chóp S.ABC có SA⊥(ABC),SA=AB=2a, tam giác ABC vuông tại B (tham khảo hình vẽ). Khoảng cách từ A đến mặt phẳng (SBC) bằng
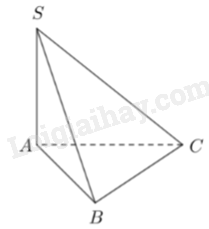
-
A.
a√2.
-
B.
a.
-
C.
2a.
-
D.
a√3.
Câu 26 : Cho chuyển động thẳng xác định bởi phương trình S=−t3+3t2+9t, trong đó t tính bằng giây và S tính bằng mét. Tính vận tốc của chuyển động tại thời điểm gia tốc triệt tiêu.
-
A.
11m/s.
-
B.
6m/s.
-
C.
12m/s.
-
D.
0m/s.
Câu 27 : Tính tổng tất cả các nghiệm nguyên của bất phương trình log(x2+2x+3)≤log6
-
A.
5.
-
B.
−5.
-
C.
7.
-
D.
4.
Câu 28 : Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, AB=a√3, AC = AA’ = a. Giá trị sin của góc giữa đường thẳng AC’ và mặt phẳng (BCC’B’) bằng
-
A.
√104.
-
B.
√63.
-
C.
√33.
-
D.
√64.
Câu 29 : Một lớp có 60 sinh viên trong đó 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một sinh viên. Tính xác suất của các biến cố sinh viên được chọn không học tiếng Anh và tiếng Pháp.
-
A.
12.
-
B.
13.
-
C.
16.
-
D.
56.
Câu 30 : Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (A′BC) tạo với đáy một góc bằng 60∘. Thể tích khối lăng trụ ABC.A'B'C' bằng:
-
A.
√3a38⋅
-
B.
3√3a38⋅
-
C.
√3a32⋅
-
D.
3√3a34⋅
Câu 31 : Cho hàm số f(x)=x3−2x2+4 có đồ thị (C). Tìm hoành độ tiếp điểm của đồ thị (C) biết tiếp tuyến có hệ số góc bằng −1.
-
A.
x=1
-
B.
x=1;x=13
-
C.
x=−1;x=−13
-
D.
x=13
Câu 32 : Tập nghiệm của bất phương trình (23)4x≤(32)2−x là?
-
A.
[25;+∞).
-
B.
(−∞;−23].
-
C.
[−23;+∞).
-
D.
(−∞;25].
Câu 33 : Trong một bài thi đánh giá tư duy gồm 10 câu hỏi trắc nghiệm khách quan, trong đó có 5 câu hỏi lĩnh vực tự nhiên và 5 câu hỏi lĩnh vực xã hội. Mỗi câu hỏi có bốn phương án trả lời và chỉ có một phương án đúng. Một học sinh đã trả lời đúng các câu hỏi thuộc lĩnh vực tự nhiên, nhưng ở lĩnh vực xã hội học sinh đó chọn ngẫu nhiên một phương án bất kì. Biết rằng, mỗi câu trả lời đúng được 1 điểm, trả lời sai không có điểm, tính xác suất học sinh đó đạt ít nhất 8 điểm?
-
A.
19,14%.
-
B.
19,53%.
-
C.
17,58%.
-
D.
10,35%.
Câu 34 : Cho hình chóp S.ABC có đáy ABC vuông tại B,AB=√2a,BC=a. Các cạnh bên bằng nhau và bằng a. Tính khoảng cách giữa hai đường thẳng SC và AB.
-
A.
a√24.
-
B.
a2.
-
C.
a√2.
-
D.
a√22.
Câu 35 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a,AD=a,ΔSAD đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi φ là góc phẳng nhị diện [S,BC,A]. Khẳng định nào sau đây là đúng?
-
A.
φ=60∘.
-
B.
tanφ=√34.
-
C.
φ=30∘.
-
D.
tanφ=√32.
Câu 36 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), ^SAB=30∘, SA=2a. Tính thể tích V của khối chóp S.ABCD.
-
A.
V=√3a36.
-
B.
V=a3.
-
C.
V=a39.
-
D.
V=a33.
Câu 37 : Tập nghiệm bất phương trình 4x−3.2x−4≥0 là
-
A.
[2;+∞).
-
B.
[4;+∞).
-
C.
(4;+∞).
-
D.
(2;+∞).
Câu 38 : Có bao nhiêu số nguyên x thoả mãn điều kiện (7x−49)(log23x−7log3x+6)<0 ?
-
A.
728.
-
B.
726.
-
C.
725.
-
D.
729.
Câu 39 : Ba cầu thủ sút phạt đến 11m, mỗi người đá một lần với xác suất làm bàn tương ứng là x, y và 0,6 (vớix>y). Biết xác suất ít nhất một trong ba cầu thủ ghi bàn là 0,976 và xác suất để cả ba cầu thủ đều ghi ban là 0,336. Tính xác suất để có đúng hai cầu thủ ghi bàn.
-
A.
P(C)=0,452
-
B.
P(C)=0,435
-
C.
P(C)=0,4525
-
D.
P(C)=0,4245
Câu 40 : Cho đa thức P(x) bậc 3 và có 3 nghiệm phân biệt x1,x2,x3. Tính 1P′(x1)+1P′(x2)+1P′(x3)
-
A.
1
-
B.
−1
-
C.
0
-
D.
Không xác định
Lời giải và đáp án
Câu 1 : Với b,c là hai số thực dương tùy ý thỏa mãn log5b≥log5c, khẳng định nào dưới đây là đúng?
-
A.
b≥c.
-
B.
b≤c.
-
C.
b>c.
-
D.
b<c.
Đáp án : A
logaf(x)≥logag(x)(∗)
Nếu a>1 thì phương trình (∗)⇔{f(x)>g(x)g(x)>0
Nếu 0<a<1 thì phương trình (∗)⇔{f(x)<g(x)f(x)>0
Chú ý: logaf(x) có nghĩa ⇔{f(x)>00<a≠1
Ta có: log5b≥log5c⇔b≥c.
Đáp án A.
Câu 2 : Đạo hàm của hàm số y=2x là:
-
A.
y′=2xln2
-
B.
y′=2x
-
C.
y′=2xln2
-
D.
y′=x2x−1
Đáp án : A
Sử dụng công thức tính đạo hàm (ax)′=axlna.
y′=(2x)′=2x.ln2
Đáp án A.
Câu 3 : Nghiệm của phương trình 2x=3 là
-
A.
x=log23.
-
B.
x=log32.
-
C.
x=3.
-
D.
x=2.
Đáp án : A
Định nghĩa logax=b⇔x=ab
2x=3⇔x=log23
Đáp án A.
Câu 4 : Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a,AA′⊥(ABCD) và AA′=3a. Thể tích của khối lăng trụ đã cho bằng
-
A.
a3.
-
B.
3a3.
-
C.
2a3.
-
D.
3a34⋅
Đáp án : B
Thể tích khối trụ V=h.B
Thể tích khối trụ VABCA′B′C′=AA′.SABCD=3a.a2=3a3
Đáp án B.
Câu 5 : Cho hình lập phương ABCD⋅A′B′C′D′ có cạnh bằng a (tham khảo hình vẽ).

Gọi φ là góc giữa hai mặt phẳng (BDA′) và (ABCD). Giá trị của sinφ bằng
-
A.
√63.
-
B.
√34.
-
C.
√33.
-
D.
√64.
Đáp án : A
^(BDA′),(ABCD)=^A′O,AO=^A′OA
Gọi O=AC∩BD. Suy ra AO⊥BD. (1)
Ta chứng minh được BD⊥A′O. (2)
Từ (1) và (2) suy ra ^(BDA′),(ABCD)=^A′O,AO=^A′OA.
Vậy sin((BDA′),(ABCD))=sin^A′OA=AA′A′O=√63.
Đáp án A.
Câu 6 : Hệ số góc tiếp tuyến của đồ thị hàm số y=2x2−2 tại điểm có hoành độ x0=2là:
-
A.
4
-
B.
8
-
C.
6
-
D.
-4
Đáp án : B
Hệ số góc tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=x0là: y=f′(x0).
Ta có: y′=4x.
Vậy hệ số góc tiếp tuyến của đồ thị hàm số y=2x2−2 tại điểm có hoành độ x0=2là: k=y′(2)=4.2=8.
Đáp án B.
Câu 7 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,SA vuông góc với đáy, SA=a. Khoảng cách giữa hai đường thẳng SB và CD là
-
A.
a.
-
B.
2a.
-
C.
a√2.
-
D.
a√3.
Đáp án : A
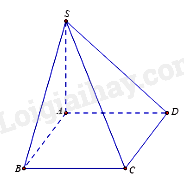
Vì DC∥AB nên d(SB;CD)=d(CD;(SAB))=d(D;(SAB))=AD=a
Đáp án A.
Câu 8 : Có hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,6. Xác suất để có ít nhất một người bắn trúng là:
-
A.
0,95.
-
B.
0,92.
-
C.
0,48.
-
D.
0.96.
Đáp án : B
Áp dụng công thức cộng và nhân xác suất.
Xác suất để không có ai bắn trúng là: (1−0,8)(1−0,6)=0,2.0,4=0,08
Xác suất để có ít nhất một người bắn trúng là: 1−0,08=0,92.
Đáp án B.
Câu 9 : Tính đạo hàm của hàm số sau y=−3x+4x−2.
-
A.
y′=2(x−2)2.
-
B.
y′=−11(x−2)2.
-
C.
y′=−5(x−2)2.
-
D.
y′=10(x−2)2.
Đáp án : A
Sử dụng quy tắc tính đạo hàm.
Ta có: y′=−3(x−2)−(−3x+4)(x−2)2=2(x−2)2
Đáp án A.
Câu 10 : Cho hình chóp S.ABC,SA vuông góc với đáy, J là hình chiếu của A trên BC. Khẳng định nào sau đây là đúng?

-
A.
BC⊥(SAJ).
-
B.
AJ⊥SC.
-
C.
BC⊥(SAC).
-
D.
BC⊥(SAB)
Đáp án : A
+Muốn chứng minh một đường thẳng vuông góc với một mặt phẳng, ta chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau cùng nằm trên mặt phẳng.
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó sẽ vuông góc với tất cả các đường thẳng nằm trong mặt phẳng.
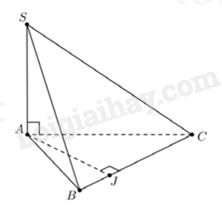
Lại có AJ⊥BC(2)(giả thiết)
Từ (1);(2)⇒BC⊥(SAJ).
Đáp án A.
Câu 11 : Có ba chiếc hộp: hộp I có 4 bi đỏ và 5 bi xanh, hộp II có 3 bi đỏ và 2 bi đen, hộp III có 5 bi đỏ và 3 bi vàng. Lấy ngẫu nhiên ra một hộp rồi lấy một viên bi từ hộp đó. Xác suất để viên bi lấy được màu đỏ bằng
-
A.
6011080.
-
B.
611.
-
C.
16.
-
D.
61360.
Đáp án : A
Sử dụng xác suất có điều kiện.
Lấy ngẫu nhiên một hộp.
Gọi C1 là biến cố lấy được hộp I;
Gọi C2 là biến cố lấy được hộp II;
Gọi C3 là biến cố lấy được hộp III.
Suy ra P(C1)=P(C2)=P(C3)=13.
Gọi C là biến cố "lấy ngẫu nhiên một hộp, trong hộp đó lại lấy ngẫu nhiên một viên bi và được bi màu đỏ”.
Ta có: C=(C∩C1)∪(C∩C2)∪(C∩C3)
⇒P(C)=P(C∩C1)+P(C∩C2)+P(C∩C3)
=13⋅49+13⋅35+13⋅58=6011080.
Đáp án A.
Câu 12 : Tập nghiệm của bất phương trình log7(5x−2)>log7(6−3x) là
-
A.
S=(1;+∞).
-
B.
S=(1;2).
-
C.
S=(2;+∞).
-
D.
S=(25;1).
Đáp án : B
Giải bất phương trình logarit cơ bản.
log7(5x−2)>log7(6−3x) điều kiện {5x−2>06−3x>0⇔25<x<2
⇔5x−2>6−3x⇔x>1
Tập nghiệm của bất phương trình là S=(1;2).
Đáp án B.
Câu 13 : Tập nghiệm của bất phương trình 5x+2<(125)−x là
-
A.
(2;+∞).
-
B.
(−∞;1).
-
C.
(−∞;2).
-
D.
(1;+∞).
Đáp án : A
Đưa bpt về cùng cơ số
5x+2<(125)−x⇔5x+2<(5−2)−x⇔5x+2<52x⇔x+2<2x⇔x>2
Vậy S=(2;+∞)
Đáp án A.
Câu 14 : Hàm số y=(1+x)√1−xcó đạo hàm y′=ax+b2√1−x. Tính a+b.
-
A.
−2.
-
B.
2.
-
C.
−3.
-
D.
1
Đáp án : A
Sử dụng quy tắc tính đạo hàm (uv)′=u′v−uv′.
y′=√1−x+(1+x)−12√1−x=2(1−x)−1−x2√1−x=1−3x2√1−x⇒{a=−3b=1⇒a+b=−3+1=−2
Đáp án A.
Câu 15 : Tìm tất cả các giá trị của tham số m để phương trình 9x−2.6x+m.4x=0 có hai nghiệm trái dấu.
-
A.
0<m<1.
-
B.
m<−1 hoặc m>1.
-
C.
m≤1.
-
D.
m<0
Đáp án : A
Chia cả hai vế cho 9x và đưa về pt bậc hai
9x−2.6x+m.4x=0 (1)
Chia cả hai vế cho 9x ta được phương trình
1−2.(23)x+m.(23)2x=0⇔mt2−2t+1=0 với t=(23)x (2)
Để (1) có 2 nghiệm trái dấu thì (2) có 2 nghiệm phân biệt thỏa mãn t1<1<t2
⇒{m≠0Δ′>0(t1−1)(t2−1)<0⇔{m≠01−m>01m−2m+1<0⇔{m≠0m<1m−1m<0⇔0<m<1
Đáp án A.
Câu 16 : Hai xạ thủ tham gia thi đấu bắn súng, mỗi người bắn vào bia của mình một viên đạn một cách độc lập với nhau. Gọi A và B lần lượt là các biến cố "Người thứ nhất bắn trúng bia"; "Người thứ hai bắn trúng bia". Khẳng định nào sau đây đúng?
-
A.
Hai biến cố A và B bằng nhau.
-
B.
Hai biến cố A và B đối nhau.
-
C.
Hai biến cố A và B độc lập với nhau.
-
D.
Hai biến cố A và B không độc lập với nhau.
Đáp án : C
Biến cố A không ảnh hưởng đến việc xác suất xảy ra biến cố B và ngược lại, thì hai biến cố A và B độc lập với nhau.
Do hai xạ thủ thi đấu một cách độc lập nên việc xảy ra biến cố A không ảnh hưởng đến việc xác suất xảy ra biến cố B và ngược lại, do đó hai biến cố A và B độc lập với nhau.
Đáp án C.
Câu 17 : Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng nhau. Gọi α là góc tạo bởi hai đường thẳng B'C và AB. Tính cosin của góc α.

-
A.
cosα=√36
-
B.
cosα=√24
-
C.
cosα=−√34
-
D.
cosα=√22
Đáp án : B
- Sử dụng a//a′⇒^(a;b)=^(a′;b).
- Sử dụng định lí cosin trong tam giác.
Ta có AB//A′B′ nên ^(B′C;AB)=^(B′C;A′B′).
Ta có: A′C=B′C=a√2 (do ACC′A′,BCC′B′ là các hình vuông cạnh a).
Áp dụng định lí Cosin trong tam giác A'B'C ta có:
cos^A′B′C=A′B2+B′C2−A′C22A′B′.B′C=a2+2a2−2a22a.a√2=√24
Vậy cos(B′C;AB)=√24.
Đáp án B.
Câu 18 : Cho (cos2x−tan3x)′=asin2x+bcos23x. Tính S=a−b?
-
A.
S=−5
-
B.
S=−1
-
C.
S=1
-
D.
S=5
Đáp án : C
- Áp dụng công thức tính đạo hàm hàm lượng giác: (coskx)′=−ksinkx, (tankx)′=kcos2kx.
- Đồng nhất hệ số tìm a, b và tính S.
Ta có: (cos2x−tan3x)′=−2sin2x−3cos23x.
⇒a=−2,b=−3.
Vậy S=a−b=−2−(−3)=1.
Đáp án C.
Câu 19 : Một chất điểm chuyển động trong 20 giây đầu tiên có phương trình s(t)=112t4−t3+6t2+10t, tròng đó t>0tính bằng giây và S(t) tính bằng mét (m). Hỏi tại thời điểm t=3s thì vận tốc của vật bằng bao nhiêu?
-
A.
18m/s.
-
B.
28m/s .
-
C.
13m/s.
-
D.
17m/s.
Đáp án : B
Nếu quãng đường vật chuyển động có phương trình S=S(t).
Khi đó, phương trình vận tốc của chuyển động là v(t)=S′(t).
Phương trình vận tốc của chuyển động là: v(t)=s′(t)=13t3−3t2+12t+10.
Do đó, tại thời điểm t=3s thì vận tốc của vật là v(3)=13.33−3.32+12.3+10=28(m/s)
Đáp án B.
Câu 20 : Câu lạc bộ cờ vua của một trường THPT có 20 thành viên ở ba khối, trong đó khối 10 có 3 nam và 2 nữ, khối 11 có 4 nam và 4 nữ, khối 12 có 5 nam và 2 nữ. Giáo viên chọn ngẫu nhiên một thành viên của câu lạc bộ để tham gia thi đấu giao hữu. Xét các biến cố sau:
A : "Thành viên được chọn là học sinh khối 11";
B : "Thành viên được chọn là học sinh nam".
Khi đó biến cố A∪B là
-
A.
"Thành viên được chọn là học sinh khối 11 và là học sinh nam".
-
B.
"Thành viên được chọn là học sinh khối 11 và không là học sinh nam".
-
C.
"Thành viên được chọn là học sinh khối 11 hoặc là học sinh nam".
-
D.
"Thành viên được chọn không là học sinh khối 11 hoặc là học sinh nam".
Đáp án : C
Theo định nghĩa, biến cố “ A hoặc B xảy ra" được gọi là biến cố hợp của A và B.
Biến cố A∪B bao gồm việc chọn thành viên là học sinh khối 11 hoặc là học sinh nam.
Đáp án C.
Câu 21 : Cho khối lăng trụ ABC⋅A′B′C′ có thể tích là 4. Khối chóp A′⋅ABC có thể tích bằng
-
A.
4.
-
B.
12.
-
C.
43.
-
D.
83.
Đáp án : C
Thể tích khối lăng trụ V=Bh.
Cho khối lăng trụ ABC⋅A′B′C′ có thể tích là 4. Khối chóp A′⋅ABC có thể tích bằng 13VABCD.A′B′C′D′=43
Đáp án C.
Câu 22 : Cho hàm số y=x3−3x2+2 có đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 3 có dạng ax+by−25=0. Khi đó, tổng a+b bằng:
-
A.
8.
-
B.
−10.
-
C.
−8.
-
D.
10.
Đáp án : A
- Tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=x0 là:
y=f′(x0)(x−x0)+f(x0)
- Đồng nhất hệ số tìm a,b và tính tổng a+b.
Ta có: y′=3x2−6x⇒y′(3)=9 và y(3)=2.
Khi đó ta có phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 3 là:
y=9(x−3)+2⇔y=9x−25⇔9x−y−25=0.
⇔{a=9b=−1. Vậy a+b=9+(−1)=8.
Đáp án A.
Câu 23 : Một hộp chứa 12 chiếc thẻ có kích thước như nhau, trong đó có 5 chiếc thẻ màu xanh được đánh số từ 1 đến 5; có 4 chiếc thẻ màu đỏ được đánh số từ 1 đến 4 và 3 chiếc thẻ màu vàng được đánh số từ 1 đến 3. Lấy ngẫu nhiên 2 chiếc thẻ từ hộp, tính xác suất để 2 chiếc thẻ được lấy vừa khác màu vừa khác số.
-
A.
2966.
-
B.
3766.
-
C.
833.
-
D.
1433.
Đáp án : B
Giả sử phép thử T có không gian mẫu n(Ω) là một tập hữu hạn và các kết quả của T là đồng khả năng. Nếu A là một biến cố liên quan với phép thử T và ΩA là một tập hợp các kết quả thuận lợi cho A thì xác suất của A là một số , kí hiệu là P(A), được xác định bởi công thức :
P(A)=n(A)n(Ω)=sophantucuaAsophantucuaΩ
Không gian mẫu là số cách lấy tùy ý 2 chiếc thẻ từ 12 chiếc thẻ ⇒ Số phần tử của không gian mẫu là n(Ω)=C212=66.
Gọi A là biến cố: “2 chiếc thẻ lấy được vừa khác màu vừa khác số”.
TH1: 1 thẻ xanh + 1 thẻ đỏ không cùng số.
Chọn 1 thẻ đỏ có 4 cách, chọn 1 thẻ xanh có 4 cách (không chọn thẻ cùng số với thẻ đỏ).
⇒ Có 4.4=16 cách.
TH2: 1 thẻ xanh + 1 thẻ vàng không cùng số.
Chọn 1 thẻ vàng có 3 cách, chọn 1 thẻ xanh có 4 cách (không chọn thẻ cùng số với thẻ vàng).
⇒ Có 3.4=12 cách.
TH3: 1 thẻ đỏ + 1 thẻ vàng không cùng số.
Chọn 1 thẻ vàng có 3 cách, chọn 1 thẻ đỏ có 3 cách (không chọn thẻ cùng số với thẻ vàng).
⇒ Có 3.3=9 cách.
⇒n(A)=16+12+9=37.
Vậy xác suất của biến cố A là: P(A)=n(A)n(Ω)=3766.
Đáp án B.
Câu 24 : Cho A,B là hai biến cố độc lập. Biết P(A)=14,P(A∩B)=19. Tính P(B)
-
A.
736.
-
B.
15.
-
C.
49.
-
D.
536.
Đáp án : C
A,B là hai biến cố độc lập nên: P(A∩B)=P(A)⋅P(B).
A,B là hai biến cố độc lập nên: P(A∩B)=P(A)⋅P(B)⇔19=14⋅P(B)⇔P(B)=49.
Đáp án C.
Câu 25 : Cho hình chóp S.ABC có SA⊥(ABC),SA=AB=2a, tam giác ABC vuông tại B (tham khảo hình vẽ). Khoảng cách từ A đến mặt phẳng (SBC) bằng

-
A.
a√2.
-
B.
a.
-
C.
2a.
-
D.
a√3.
Đáp án : A
Kẻ AH⊥SB(H∈SB). Chứng minh AH⊥(SBC)
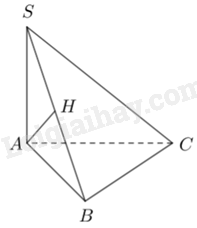
Ta có: SA⊥BCAB⊥BC}⇒(SAB)⊥BC⇒(SAB)⊥(SBC)
⇒AH⊥(SBC)Ta có: AH=SA.AB√SA2+AB2=2a.2a√4a2+4a2=a√2
Đáp án A.
Câu 26 : Cho chuyển động thẳng xác định bởi phương trình S=−t3+3t2+9t, trong đó t tính bằng giây và S tính bằng mét. Tính vận tốc của chuyển động tại thời điểm gia tốc triệt tiêu.
-
A.
11m/s.
-
B.
6m/s.
-
C.
12m/s.
-
D.
0m/s.
Đáp án : C
- Tìm v=s′(t), a=v′(t)=s″(t).
- Giải phương trình a(t)=0 tìm thời điểm gia tốc triệt tiêu.
- Thay t vừa tìm được tính giá trị vận tốc tại đó.
Ta có
v(t)=S′(t)=−3t2+6t+9a(t)=v′(t)=−6t+6
Thời điểm gia tốc triệt tiêu thỏa mãn a(t)=0⇔−6t+6=0⇔t=1.
Vậy vận tốc tại thời điểm gia tốc triệt tiêu là v(1)=−3.12+6.1+9=12(m/s).
Đáp án C.
Câu 27 : Tính tổng tất cả các nghiệm nguyên của bất phương trình log(x2+2x+3)≤log6
-
A.
5.
-
B.
−5.
-
C.
7.
-
D.
4.
Đáp án : B
Giải bất phương trình
Ta có: log(x2+2x+3)≤log6
⇔x2+2x+3≤6⇔x2+2x−3≤0⇔−3≤x≤1
Mà x∈Z⇒x∈{−3;−2;−1;0;1}
Vậy tổng các nghiệm bằng −5.
Đáp án B.
Câu 28 : Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, AB=a√3, AC = AA’ = a. Giá trị sin của góc giữa đường thẳng AC’ và mặt phẳng (BCC’B’) bằng
-
A.
√104.
-
B.
√63.
-
C.
√33.
-
D.
√64.
Đáp án : D
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu vuông góc của đường thẳng trên mặt phẳng.
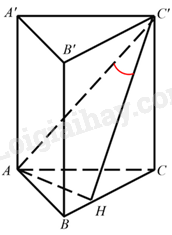
Xét ΔABC vuông tại A:1AH2=1AB2+1AC2⇔AH=√32a.
Xét ΔAA′C′ vuông tại C’: AC′=√AA′2+AC′2=a√2.
Xét ΔAHC′ vuông tại C’: sin^AC′H=AHAC′=√64.
Đáp án D.
Câu 29 : Một lớp có 60 sinh viên trong đó 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một sinh viên. Tính xác suất của các biến cố sinh viên được chọn không học tiếng Anh và tiếng Pháp.
-
A.
12.
-
B.
13.
-
C.
16.
-
D.
56.
Đáp án : C
Tính biến cố đối.
Gọi A : "Sinh viên được chọn học tiếng Anh";
B : "Sinh viên được chọn chỉ học tiếng Pháp";
D : "Sinh viên được chọn không học tiếng Anh và tiếng Pháp ".
Ta có:
Rõ ràng P(A)=4060=23,P(B)=3060=12 và P(A∩B)=2060=13.
Từ đó P(A∪B)=P(A)+P(B)−P(A∩B)=23+12−13=56
và P(D)=P(ˉA∩ˉB)=P(¯A∪B)=1−P(A∪B)=1−56=16.
Câu 30 : Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (A′BC) tạo với đáy một góc bằng 60∘. Thể tích khối lăng trụ ABC.A'B'C' bằng:
-
A.
√3a38⋅
-
B.
3√3a38⋅
-
C.
√3a32⋅
-
D.
3√3a34⋅
Đáp án : B
V=AA′.SABC
⇒(A′AM)⊥BC⇒A′M⊥BC
Do đó, ^A′AM=((A′BC);(ABC))=60o.
Dễ thấy A′A=AM.tan60o=a√32.√3=3a2.
Do đó, thể tích đa diện là V=AA′.SABC=3a2.a2√34=3a3√38.
Đáp án B.
Câu 31 : Cho hàm số f(x)=x3−2x2+4 có đồ thị (C). Tìm hoành độ tiếp điểm của đồ thị (C) biết tiếp tuyến có hệ số góc bằng −1.
-
A.
x=1
-
B.
x=1;x=13
-
C.
x=−1;x=−13
-
D.
x=13
Đáp án : B
Hệ số góc của tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=x0 là k=f′(x0).
Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x=x0 là f′(x)=3x20−4x0=−1.
⇔x0=1 hoặc x0=13.
Đáp án B.
Câu 32 : Tập nghiệm của bất phương trình (23)4x≤(32)2−x là?
-
A.
[25;+∞).
-
B.
(−∞;−23].
-
C.
[−23;+∞).
-
D.
(−∞;25].
Đáp án : C
Đưa về cùng cơ số.
ax≤ay⇔x≥y khi 0<a<1.
Ta có
(23)4x≤(32)2−x⇔(23)4x≤(23)x−2⇔4x≥x−2⇔3x≥−2⇔x≥−23
Vậy tập nghiệm của bất phương trình là [−23;+∞).
Đáp án C.
Câu 33 : Trong một bài thi đánh giá tư duy gồm 10 câu hỏi trắc nghiệm khách quan, trong đó có 5 câu hỏi lĩnh vực tự nhiên và 5 câu hỏi lĩnh vực xã hội. Mỗi câu hỏi có bốn phương án trả lời và chỉ có một phương án đúng. Một học sinh đã trả lời đúng các câu hỏi thuộc lĩnh vực tự nhiên, nhưng ở lĩnh vực xã hội học sinh đó chọn ngẫu nhiên một phương án bất kì. Biết rằng, mỗi câu trả lời đúng được 1 điểm, trả lời sai không có điểm, tính xác suất học sinh đó đạt ít nhất 8 điểm?
-
A.
19,14%.
-
B.
19,53%.
-
C.
17,58%.
-
D.
10,35%.
Đáp án : D
Chia trường hợp và tính xác suất
Học sinh trả lời hết tất cả các câu thuộc KHTN là đã được 5 điểm.
Để được ít nhất 8 điểm thì học sinh đó phải trả lời đúng ít nhất 3 câu thuộc KHXH.
TH1: 3 câu đúng, 2 câu sai: C35⋅(14)3(34)2
TH2: 4 câu đúng, 1 câu sai: C45⋅(14)4(34)
TH3: 5 câu đúng: C55⋅(14)5
Vậy C35⋅(14)3(34)2+C45⋅(14)4(34)+C55⋅(14)5≈0,1035≈10,35%
Đáp án D.
Câu 34 : Cho hình chóp S.ABC có đáy ABC vuông tại B,AB=√2a,BC=a. Các cạnh bên bằng nhau và bằng a. Tính khoảng cách giữa hai đường thẳng SC và AB.
-
A.
a√24.
-
B.
a2.
-
C.
a√2.
-
D.
a√22.
Đáp án : D
Đưa về khoảng cách từ 1 điểm đến một mặt phẳng
Do ΔABC vuông tại B nên H là tâm đường tròn ngoại tiếp ΔABC
Do SA=SB=SC⇒SH⊥(ABC)
Trong (ABC) dựng hình bình hành ABCD⇒d(AB,CD)=d(AB,SCD)=d(A,SCD)=2d(H,SCD)
Kẻ HM⊥CD,HN⊥SM⇒d(H,SCD)=HNAC=a√3
⇒HA=HC=a√32⇒SH=a2
HM=12AD=12BC=a2⇒1HN2=1HM2+1SH2⇒HN=√24a⇒d(AB,CD)=√22a
Đáp án D.
Câu 35 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a,AD=a,ΔSAD đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi φ là góc phẳng nhị diện [S,BC,A]. Khẳng định nào sau đây là đúng?
-
A.
φ=60∘.
-
B.
tanφ=√34.
-
C.
φ=30∘.
-
D.
tanφ=√32.
Đáp án : A
Xác định góc giữa hai mặt phẳng tạo thành.
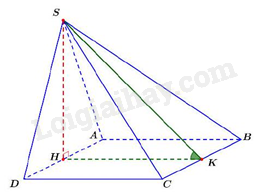
Suy ra SH⊥(ABCD) và HK⊥BC.
Khi đó: {BC⊥HKBC⊥SH⇒BC⊥(SHK)⇒BC⊥SK.
Ta có: {(SBC)∩(ABC)=BCHK⊥BCSK⊥BC⇒[S,BC,A]=^SKH=φ.
Xét vuông tại H, ta có:
tanφ=tan^SKH=SHHK=√3⇒φ=60∘.
Đáp án A.
Câu 36 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), ^SAB=30∘, SA=2a. Tính thể tích V của khối chóp S.ABCD.
-
A.
V=√3a36.
-
B.
V=a3.
-
C.
V=a39.
-
D.
V=a33.
Đáp án : D
VS.ABCD=13SH.SABCD
Dựng SH⊥AB, do (SAB)⊥(ABCD)⇒SH⊥(ABCD).
Ta có, do ΔSHA vuông tại H: sin^SAH=SHSA⇔SH=SA.sin^SAH=a
SABCD=a2.
Vậy VS.ABCD=13SH.SABCD=a33.
Đáp án D.
Câu 37 : Tập nghiệm bất phương trình 4x−3.2x−4≥0 là
-
A.
[2;+∞).
-
B.
[4;+∞).
-
C.
(4;+∞).
-
D.
(2;+∞).
Đáp án : A
Phân tích thành nhân tử và giải bất phương trình
Ta có
4x−3.2x−4≥0⇔(2x−4)(2x+1)≥0⇔2x−4≥0⇔2x≥4⇔x≥2
Đáp án A.
Câu 38 : Có bao nhiêu số nguyên x thoả mãn điều kiện (7x−49)(log23x−7log3x+6)<0 ?
-
A.
728.
-
B.
726.
-
C.
725.
-
D.
729.
Đáp án : B
Giải bất phương trình A.B<0⇔[{A>0B<0{A<0B>0.
Điều kiện: x>0
(7x−49)(log23x−7log3x+6)<0⇔[{7x−49>0log23x−7log3x+6<0{7x−49<0log23x−7log3x+6>0
[{7x>491<log3x<6⇔[7x<49{x>23<x<36⇔[log3x<1log3x>6]{x<2[0<x<3x>36
⇔[0<x<23<x<36
Mà x∈Z⇒x∈{1;4;5;…;728}
Vậy có 726 số thỏa mãn.
Đáp án B.
Câu 39 : Ba cầu thủ sút phạt đến 11m, mỗi người đá một lần với xác suất làm bàn tương ứng là x, y và 0,6 (vớix>y). Biết xác suất ít nhất một trong ba cầu thủ ghi bàn là 0,976 và xác suất để cả ba cầu thủ đều ghi ban là 0,336. Tính xác suất để có đúng hai cầu thủ ghi bàn.
-
A.
P(C)=0,452
-
B.
P(C)=0,435
-
C.
P(C)=0,4525
-
D.
P(C)=0,4245
Đáp án : A
Đây là bài toán ngược :
Phương pháp : xây dựng được phương trình từ đó giải xác suât ban đầu
Sử dụng tính chất nhân xác suất khi A1,A2....Anlà các biến cố độc lập nhau ta có công thức nhân xác suất :
P(A1∩A2....∩An)=P(A1).P(A2)...P(An)
Gọi Ai là biến cố “người thứ i ghi bàn” với i=1;2;3.
Ta có các Ai độc lập với nhau và P(A1)=x,P(A2)=y,P(A3)=0,6.
Gọi A là biến cố: “ Có ít nhất một trong ba cầu thủ ghi bàn”
B: “ Cả ba cầu thủ đều ghi bàn”
C: “Có đúng hai cầu thủ ghi bàn”
Ít nhất 1 trong 3 cầu thử ghi bàn : lấy tổng số trường hợp trừ đi trường hợp tất cả đều không ghi bàn :
Ta có: số TH tất cả các cầu thủ không ghi bàn : ˉA=¯A1.¯A2.¯A3⇒P(ˉA)=P(¯A1).P(¯A2).P(¯A3)=0,4(1−x)(1−y)
Nên Ít nhất 1 trong 3 cầu thủ ghi bàn là : P(A)=1−P(ˉA)=1−0,4(1−x)(1−y)=0,976
⇔(1−x)(1−y)=350⇔xy−x−y=−4750 (1).
Tương tự: cả 3 cầu thủ ghi bàn :B=A1.A2.A3, suy ra:
P(B)=P(A1).P(A2).P(A3)=0,6xy=0,336 hay là xy=1425 (2)
Từ (1) và (2) ta có hệ: {xy=1425x+y=32⇔{y=32−xx2−32x+1425=0⇔[{x=0,8y=0,7{x=0,7y=0,8
Theo giả thiết ta có x>y⇒{x=0,8y=0,7.
Ta có: TH có đúng 2 cầu thủ ghi bàn :C=¯A1A2A3+A1¯A2A3+A1A2¯A3
Nên P(C)=(1−x)y.0,6+x(1−y).0,6+xy.0,4=0,452.
Đáp án A.
Câu 40 : Cho đa thức P(x) bậc 3 và có 3 nghiệm phân biệt x1,x2,x3. Tính 1P′(x1)+1P′(x2)+1P′(x3)
-
A.
1
-
B.
−1
-
C.
0
-
D.
Không xác định
Đáp án : C
+) Do P(x) bậc 3 và có 3 nghiệm phân biệt x1,x2,x3 nên P(x) được biểu diễn dưới dạng P(x)=a(x−x1)(x−x2)(x−x3)(a≠0).
+) Tính P′(x), từ đó tính P′(x1);P′(x2);P′(x3).
+) Thay vào biểu thức 1P′(x1)+1P′(x2)+1P′(x3). Quy đồng và rút gọn.
Do P(x) bậc 3 và có 3 nghiệm phân biệt x1,x2,x3 nên P(x) được biểu diễn dưới dạng P(x)=a(x−x1)(x−x2)(x−x3)(a≠0).
Ta có: P′(x)=a(x−x2)(x−x3)+a(x−x1)(x−x3)+a(x−x1)(x−x2)
⇒{P(x1)=a(x1−x2)(x1−x3)P(x2)=a(x2−x1)(x2−x3)P(x3)=a(x3−x1)(x3−x2)⇒1P′(x1)+1P′(x2)+1P′(x3)=1a(x1−x2)(x1−x3)+1a(x2−x1)(x2−x3)+1a(x3−x1)(x3−x2)=−x2+x3−x3+x1−x1+x2a(x1−x2)(x2−x3)(x3−x1)=0
Đáp án C.
Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
A. NỘI DUNG ÔN TẬP I. Đại số 1. Hàm số mũ và hàm số logarit - Lũy thừa với số mũ thực - Logarit - Hàm số mũ và hàm số logarit - Phương trình, bất phương trình mũ và logarit
>> 2K8! chú ý! Mở đặt chỗ Lộ trình Sun 2026: Luyện thi chuyên sâu TN THPT, Đánh giá năng lực, Đánh giá tư duy tại Tuyensinh247.com (Xem ngay lộ trình). Ưu đãi -70% (chỉ trong tháng 3/2025) - Tặng miễn phí khoá học tổng ôn lớp 11, 2K8 xuất phát sớm, X2 cơ hội đỗ đại học. Học thử miễn phí ngay.
 |
 |
 |
 |
 |
 |
 |
 |









