Phương pháp giải:

Sử dụng phương pháp hình học để tính giá trị của P.

Chú ý: \(\left| {\dfrac{{{z_1}}}{{{z_2}}}} \right| = \dfrac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}}\), \({a^2} = {b^2} + {c^2} - 2bc\cos A\)

Lời giải chi tiết:

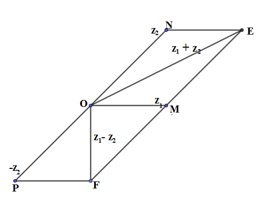
Ta có: \(P = \left| {\dfrac{{{z_1} + {z_2}}}{{{z_1} - {z_2}}}} \right| = \dfrac{{\left| {{z_1} + {z_2}} \right|}}{{\left| {{z_1} - {z_2}} \right|}} = \dfrac{{OE}}{{OF}}\) (quan sát hình vẽ)

\(\begin{array}{l}O{E^2} = O{M^2} + M{E^2} - 2OM.ME.\cos {135^0} = 2 + 4 - 2\sqrt 2 .2.\left( { - \dfrac{{\sqrt 2 }}{2}} \right) = 10\\ \Rightarrow OE = \sqrt {10} \end{array}\)

\(\begin{array}{l}O{F^2} = O{M^2} + M{F^2} - 2OM.MF.\cos {45^0} = 2 + 4 - 2\sqrt 2 .2.\dfrac{{\sqrt 2 }}{2} = 2\\ \Rightarrow OF = \sqrt 2 \end{array}\)

\( \Rightarrow P = \dfrac{{OE}}{{OF}} = \sqrt 5 \).

Chọn: A