Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình bên:
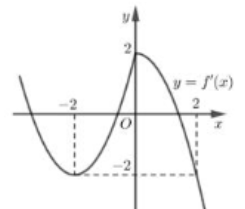
Hàm số \(y = f\left( {x + 1} \right) + {x^2} + 2x\) đồng biến trên khoảng
- A (-2;-1)
- B (-3;-2)
- C (-1;0)
- D (0;1)
- E Cả C và D đều đúng
Phương pháp giải:
- Tính đạo hàm hàm số.
- Xét phương trình \(y' = 0\), sử dụng tương giao đồ thị hàm số.
- Đặt ẩn phụ \(t = x + 1\), dựa vào các đáp án và đồ thị hàm số xác định dấu của \(y'\).
Lời giải chi tiết:
Đặt \(g\left( x \right) = f\left( {x + 1} \right) + {x^2} + 2x\) ta có \(g'\left( x \right) = f'\left( {x + 1} \right) + 2x + 2 = f'\left( {x + 1} \right) + 2\left( {x + 1} \right)\).
Đặt \(t = x + 1\) ta có \(g'\left( {t - 1} \right) = f'\left( t \right) + 2t\).
Xét phương trình \(g'\left( x \right) = 0 \Leftrightarrow g'\left( {t - 1} \right) = 0 \Leftrightarrow f'\left( t \right) = - 2t\).
Vẽ đồ thị hàm số \(y = f'\left( t \right)\) và \(y = - 2t\) trên cùng mặt phẳng tọa độ ta có:
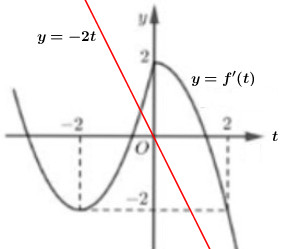
+ Xét đáp án A: \(x \in \left( { - 2; - 1} \right) \Rightarrow t \in \left( { - 1;0} \right)\).
Trên khoảng \(\left( { - 1;0} \right)\) đồ thị hàm số \(y = f'\left( t \right)\) có lúc nằm trên có lúc nằm dưới đồ thị hàm số \(y = - 2t\), do đó hàm số \(y = g\left( x \right)\) có lúc đồng biến có lúc nghịch biến.
+ Xét đáp án B: \(x \in \left( { - 3; - 2} \right) \Rightarrow t \in \left( { - 2; - 1} \right)\).
Trên khoảng \(\left( { - 2; - 1} \right)\) đồ thị hàm số \(y = f'\left( t \right)\) nằm hoàn toàn phía dưới đồ thị hàm số \(y = - 2t\), do đó hàm số \(y = g\left( x \right)\) nghịch biến trên \(\left( { - 3; - 2} \right)\).
+ Xét đáp án C: \(x \in \left( { - 1;0} \right) \Rightarrow t \in \left( {0;1} \right)\).
Trên khoảng \(\left( {0;1} \right)\) đồ thị hàm số \(y = f'\left( t \right)\) nằm hoàn toàn phía trên đồ thị hàm số \(y = - 2t\), do đó hàm số \(y = g\left( x \right)\) đồng biến trên \(\left( { - 1;0} \right)\).
+ Xét đáp án D: \(x \in \left( {0;1} \right) \Rightarrow t \in \left( {1;2} \right)\).
Trên khoảng \(\left( {1;2} \right)\) đồ thị hàm số \(y = f'\left( t \right)\) nằm hoàn toàn phía trên đồ thị hàm số \(y = - 2t\), do đó hàm số \(y = g\left( x \right)\) đồng biến trên \(\left( {0;1} \right)\).
Vậy cả đáp án C và D đều đúng.
Chọn E.







