Câu hỏi
Cho hàm số \(f\left( x \right)\) có đồ thị trên đoạn \(\left[ { - 3;3} \right]\) là đường gấp khúc ABCD như hình vẽ.
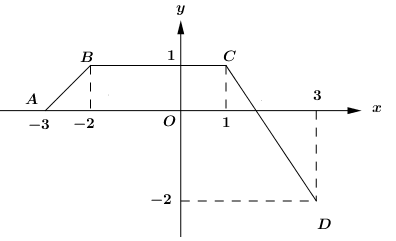
Tính \(\int\limits_{ - 3}^3 {f\left( x \right)dx} \).
- A \(\dfrac{5}{2}\)
- B \(\dfrac{{35}}{6}\)
- C \(\dfrac{{ - 5}}{2}\)
- D \(\dfrac{{ - 35}}{6}\)
Phương pháp giải:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox trên \(\left[ { - 3;3} \right]\).
Lời giải chi tiết:
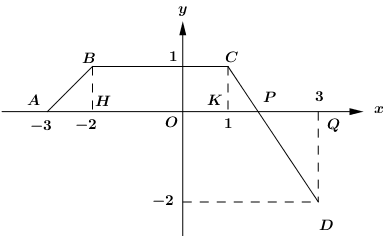
Ta có:
\(\begin{array}{l}\int\limits_{ - 3}^3 {f\left( x \right)dx} = {S_{ABH}} + {S_{BCKH}} + {S_{CPK}} - {S_{DPQ}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}.1.1 + 3.1 + \dfrac{1}{2}.1.\dfrac{2}{3} - \dfrac{1}{2}.\dfrac{4}{3}.2 = \dfrac{5}{2}\end{array}\).
Chọn A.
Câu hỏi trước
