Phương pháp giải:

- Giải các phương trình hoành độ giao điểm để xác định các cận.

- Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\,\,y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).

Lời giải chi tiết:

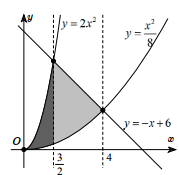
Xét các phương trình hoành độ giao điểm:

\(\begin{array}{l}2{x^2} = \dfrac{{{x^2}}}{8} \Leftrightarrow x = 0\\2{x^2} =  - x + 6 \Leftrightarrow x = \dfrac{3}{2}\,\,\left( {x \ge 0} \right)\\\dfrac{{{x^2}}}{8} =  - x + 6 \Leftrightarrow x = 4\,\,\left( {x \ge 0} \right)\end{array}\)

Vậy \(S = \int\limits_0^{\dfrac{3}{2}} {\left( {2{x^2} - \dfrac{{{x^2}}}{8}} \right)dx}  + \int\limits_{\dfrac{3}{2}}^4 {\left( { - x + 6 - \dfrac{{{x^2}}}{8}} \right)dx}  = \dfrac{{185}}{{24}}\).

Chọn C.