Câu hỏi
Cho hàm số \(f\left( x \right)\). Biết hàm số \(y = f'\left( x \right)\) có đồ thị như hình bên. Trên đoạn \(\left[ { - 4;3} \right]\), hàm số \(g\left( x \right) = 2f\left( x \right) + {\left( {1 - x} \right)^2}\) đạt giá trị nhỏ nhất tại điểm:
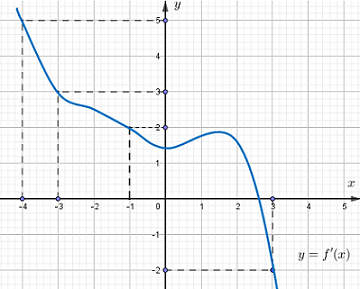
- A \({x_0} = - 4\)
- B \({x_0} = - 1\)
- C \({x_0} = 3\)
- D \({x_0} = - 3\)
Phương pháp giải:
- Tính \(g'\left( x \right)\) và tìm nghiệm của \(g'\left( x \right) = 0\) trong đoạn \(\left[ { - 4;3} \right]\).
- Tính giá trị của hàm số \(y = g\left( x \right)\) tại các điểm \( - 4;3\) và các điểm làm cho \(g'\left( x \right) = 0\).
- So sánh các giá trị trên và kết luận GTNN.
Lời giải chi tiết:
Ta có: \(g'\left( x \right) = 2f'\left( x \right) - 2\left( {1 - x} \right) = 2\left[ {f'\left( x \right) - 1 + x} \right]\).
\(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = 1 - x\).
Từ hình vẽ ta thấy, trên đoạn \(\left[ { - 4;3} \right]\) thì đường thẳng \(y = 1 - x\) cắt đồ thị hàm số \(y = f'\left( x \right)\) tại \(3\) điểm lần lượt có hoành độ \( - 4; - 1;3\) nên ta so sánh các giá trị \(g\left( { - 4} \right),g\left( { - 1} \right),g\left( 3 \right)\).
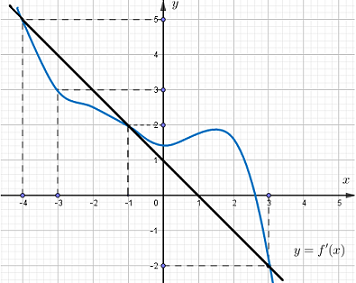
Ta thấy: \({S_1} = \int\limits_{ - 4}^{ - 1} {\left[ {1 - x - f'\left( x \right)} \right]dx} = \int\limits_{ - 4}^{ - 1} {\left[ { - g'\left( x \right)} \right]dx} = g\left( { - 4} \right) - g\left( { - 1} \right) > 0 \Rightarrow g\left( { - 4} \right) > g\left( { - 1} \right)\).
\({S_2} = \int\limits_{ - 1}^3 {\left[ {f'\left( x \right) - 1 + x} \right]dx} = \int\limits_{ - 1}^3 {\left[ {g'\left( x \right)} \right]dx} = g\left( 3 \right) - g\left( { - 1} \right) > 0 \Rightarrow g\left( 3 \right) > g\left( { - 1} \right)\).
Do đó \(g\left( { - 1} \right)\) là GTNN của hàm số \(y = g\left( x \right)\) hay hàm số đạt GTNN tại \({x_0} = - 1\).
Chọn B







