Nghiệm của phương trình \({\log _2}(x - 1) = 3\) là
-
A.
x = 10
-
B.
x = 8
-
C.
x = 9
-
D.
x = 7
\({\log _a}b = x \Leftrightarrow \left\{ \begin{array}{l}b > 0\\b = {a^x}\end{array} \right.\).
\({\log _2}(x - 1) = 3 \Leftrightarrow \left\{ \begin{array}{l}x - 1 > 0\\x - 1 = {2^3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 1\\x = 9\end{array} \right. \Leftrightarrow x = 9\).
Đáp án : C

Các bài tập cùng chuyên đề
Giải các phương trình sau:
a) \(4 - \log \left( {3 - x} \right) = 3;\)
b) \({\log _2}\left( {x + 2} \right) + {\log _2}\left( {x - 1} \right) = 1.\)
Xét phương trình \(2{\log _2}x = - 3.\)
a) Từ phương trình trên, hãy tính \({\log _2}x.\)
b) Từ kết quả ở câu a và sử dụng định nghĩa lôgarit, hãy tìm x.
Giải các phương trình sau:
a) \(\log \left( {x + 1} \right) = 2;\)
b) \(2{\log _4}x + {\log _2}\left( {x - 3} \right) = 2;\)
c) \(\ln x + \ln \left( {x - 1} \right) = \ln 4x;\)
d) \({\log _3}\left( {{x^2} - 3x + 2} \right) = {\log _3}\left( {2x - 4} \right).\)
Tính nồng độ ion hydrogen (tính bằng mol/lít) của một dung dịch có độ pH là 8.
Giải các phương trình sau:
a) \({\log _{\frac{1}{2}}}\left( {x - 2} \right) = - 2\);
b) \({\log _2}\left( {x + 6} \right) = {\log _2}\left( {x + 1} \right) + 1\)
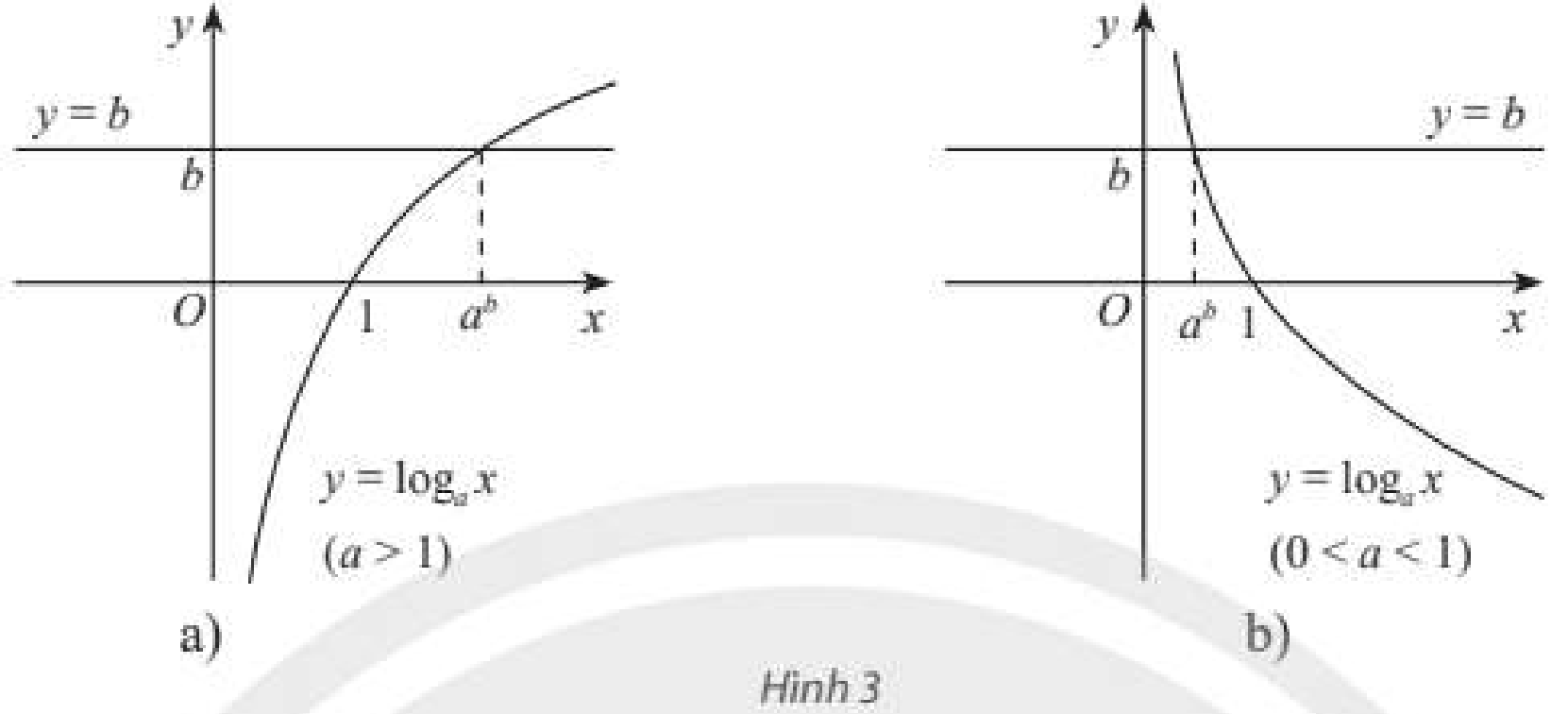
Cho đồ thị của hai hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) và \(y = b\) như Hình 3a (với \(a > 1\)) hay Hình 3b (với \(0 < a < 1\)). Từ đây hãy nhận xét về số nghiệm và công thức nghiệm của phương trình \({\log _a}x = b\).
Nhắc lại rằng, độ pH của một dung dịch được tính theo công thức \(pH = - \log x\), trong đó \(x\) là nồng độ ion H+ tính bằng mol/L.
Biết sữa có độ pH là 6,5. Nồng độ H+ của sữa bằng bao nhiêu?
Giải các phương trình sau:
a) \({\log _6}\left( {4{\rm{x}} + 4} \right) = 2\);
b) \({\log _3}x - {\log _3}\left( {x - 2} \right) = 1\).
Nếu \(\log x = 2\log 5 - \log 2\) thì
A. \(x = 8\).
B. \(x = 23\).
C. \(x = 12,5\).
D. \(x = 5\).
Giải mỗi phương trình sau:
a) \({\log _5}\left( {2x - 4} \right) + {\log _{\frac{1}{5}}}\left( {x - 1} \right) = 0\).
b) \({\log _2}x + {\log _4}x = 3\).
a) Vẽ đồ thị hàm số \(y = {\log _4}x\) và đường thẳng y = 5.
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({\log _4}x = 5\).
Cho hai ví dụ về phương trình logarit.
Nghiệm của phương trình \({\log _{0,5}}(2 - x) = - 1\) là
A. 0
B. 2,5
C. 1,5
D. 2
Giải các phương trình lôgarit sau:
a) \({\rm{lo}}{{\rm{g}}_3}\left( {4x - 1} \right) = 2\);
b) \({\rm{lo}}{{\rm{g}}_2}\left( {{x^2} - 1} \right) = {\rm{lo}}{{\rm{g}}_2}\left( {3x + 3} \right)\);
c) \({\rm{lo}}{{\rm{g}}_x}81 = 2\);
d) \({\rm{lo}}{{\rm{g}}_2}{8^x} = - 3\).
Tập nghiệm của phương trình \({\rm{lo}}{{\rm{g}}_2}\left[ {x\left( {x - 1} \right)} \right] = 1\) là
A. \(\left\{ { - 1} \right\}\).
B. \(\left\{ { - 2} \right\}\).
C. \(\left\{ { - 1;2} \right\}\).
D. \(\left\{ {\frac{{ - 1 - \sqrt 5 }}{2};\frac{{ - 1 + \sqrt 5 }}{2}} \right\}\).
Cent âm nhạc là một đơn vị trong thang lôgarit của cao độ hoặc khoảng tương đối. Một quãng tám bằng 1200 cent. Công thức xác định chênh lệch khoảng thời gian (tính bằng cent) giữa hai nốt nhạc có tần số a và \(b\) là
\(n = 1200 \cdot {\rm{lo}}{{\rm{g}}_2}\frac{a}{b}{\rm{\;}}{\rm{.}}\)
(Theo Algebra 2, NXB MacGraw-Hill, 2008)
a) Tìm khoảng thời gian tính bằng cent khi tần số thay đổi từ \(443{\rm{\;Hz}}\) về \(415{\rm{\;Hz}}\).
b) Giả sử khoảng thời gian là 55 cent và tần số đầu là \(225{\rm{\;Hz}}\), hãy tìm tần số cuối cùng.
Nghiệm của phương trình \({\log _{\frac{1}{2}}}\left( {x - 1} \right) = - 2\) là:
A. \(x = 2.\)
B. \(x = 5.\)
C. \(x = \frac{5}{2}.\)
D. \(x = \frac{3}{2}.\)
Số nghiệm của phương trình \(\log \left( {{x^2} - 7x + 12} \right) = \log \left( {2x - 8} \right)\) là:
A. \(0.\)
B. \(1.\)
C. \(2.\)
D. \(3.\)
Giải mỗi phương trình sau:
a) \({\log _4}\left( {x - 4} \right) = - 2;\)
b) \({\log _3}\left( {{x^2} + 2x} \right) = 1;\)
c) \({\log _{25}}\left( {{x^2} - 4} \right) = \frac{1}{2};\)
d) \({\log _9}\left[ {{{\left( {2x - 1} \right)}^2}} \right] = 2;\)
e) \(\log \left( {{x^2} - 2x} \right) = \log \left( {2x - 3} \right);\)
g) \({\log _2}{x^2} + {\log _{\frac{1}{2}}}\left( {2x + 8} \right) = 0.\)
Tốc độ của gió S (dặm/giờ) gần tâm của một cơn lốc xoáy được tính bởi công thức: \(S = 93\log d + 65,\) trong đó d (dặm) là quãng đường cơn lốc xoáy đó di chuyển được.
(Nguồn: Ron Larson, Intermediate Algebra, Cengage)
Tính quãng đường cơn lốc xoáy đã di chuyển được, biết tốc độ của gió ở gần tâm bằng 140 dặm/giờ (làm tròn kết quả đến hàng phần mười).
Nghiệm của phương trình \({\log _{\frac{1}{3}}}x = - 2\) là:
A. \(x = - \frac{1}{9}.\)
B. \(x = \frac{1}{9}.\)
C. \(x = 9.\)
D. \(x = - 9.\)
Nghiệm của phương trình \({\log _5}\left( {2x - 3} \right) - {\log _{\frac{1}{5}}}\left( {2x - 3} \right) = 0\) là:
A. \(x = \frac{3}{2}.\)
B. \(x = 8.\)
C. \(x = 2.\)
D. \(x = 1.\)
Với nước biển có nồng độ muối 30%, nhiệt độ T (0C) của nước biển được tinh bởi công thức \(T = 7,9\ln \left( {1,0245 - d} \right) + 61,84,\)ở đó \(d\left( {{\rm{g/c}}{{\rm{m}}^{\rm{3}}}} \right)\) là khối lượng riêng của nước biển.
(Nguồn: Ron Larson, Intermediate Algebra, Cengage)
Biết vùng biển khơi mặt ở một khu vực có nồng độ muối 30% và nhiệt độ là 8 0C. Tính khối lượng riêng của nước biển ở vùng biển đó (làm tròn kết quả đến hàng phần chục nghìn).
Cường độ của một trận động đất, kí hiệu là M (độ Richter), được cho bởi công thức \(M = \log A - \log {A_0},\) ở đó \(A\) là biên độ rung chấn tối đa đo được bằng địa chấn kế và \({A_0}\) là biên độ chuẩn (hằng số phụ thuộc vào từng khu vực)
(Nguồn: https://vi.wikipedia.org/wiki/Độ_Rickter)
Vào hồi 12 giờ 14 phút trưa ngày 27/07/2020, tại khu vực huyện Mộc Châu, Sơn La xảy ra trận động đất thứ nhất với cường độ 5,3 độ Richter. Trong vòng 20 tiếng đồng hồ, Sơn La đã xảy ra liên tiếp 7 trận động đất. Đến 8 giờ 26 phút sáng 28/07/2020, trận động đất thứ bảy xảy ra với cường độ 4 độ Richter.
(Nguồn: https://plo.vn/7-tran-dong-dat-lien-tiep-o-son-la-trong-wong-20-tieng-dong-ho-post585443.html)
Biết rằng biên độ chuẩn được dùng cho cả tỉnh Sơn La. Hỏi biên độ rung chấn tối đa của trận động đất thứ nhất gấp khoảng mấy lần biên độ rung chấn tối đa của trận động đất thứ bảy (làm tròn kết quả đến hàng đơn vị)?
Giải các phương trình sau:
a) \({\log _3}\left( {2x - 1} \right) = 3\);
b) \({\log _{49}}x = 0,25\);
c) \({\log _2}\left( {3x + 1} \right) = {\log _2}\left( {2x - 4} \right)\);
d) \({\log _5}\left( {x - 1} \right) + {\log _5}\left( {x - 3} \right) = {\log _5}\left( {2x + 10} \right)\);
e) \(\log x + \log \left( {x - 3} \right) = 1\);
g) \({\log _2}\left( {{{\log }_{81}}x} \right) = - 2\).
Cho hàm số \(y = f\left( x \right) = {\log _2}x\). Biết rằng \(f\left( b \right) - f\left( a \right) = 5\left( {a,b > 0} \right)\), tìm giá trị của \(\frac{b}{a}\).
Độ pH của một dung dịch được tính theo công thức \(pH = - \log x\), trong đó x là nồng độ ion \({H^ + }\) của dung dịch đó tính bằng mol/L. Biết rằng độ pH của dung dịch A lớn hơn độ pH của dung dịch B là 0,7. Dung dịch B có nồng độ ion \({H^ + }\) gấp bao nhiêu lần nồng độ ion \({H^ + }\) của dung dịch A?
Giả sử \(\alpha \) và \(\beta \) là hai nghiệm của phương trình \({\log _2}x.{\log _2}3x = - \frac{1}{3}\). Khi đó tích \(\alpha \beta \) bằng
A. \(\frac{1}{3}\)
B. 3
C. \(\sqrt 3 \)
D. \({\log _2}3\)
Giải phương trình \({\log _5}\left( {4x + 5} \right) = 2 + {\log _5}\left( {x - 4} \right)\)
A. 9
B. 15
C. 4
D. 5
Biết rằng \({\log _3}4.{\log _4}8.{\log _8}x = {\log _8}64\). Giá trị của x là
A. \(\frac{9}{2}\)
B. 9
C. 27
D. 81






