Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều S.ABCD cạnh bên bằng 200 m, góc \(\widehat {ASB} = {15^o}\) bằng đường gấp khúc dây đèn led vòng quanh kim tự tháp AEFGHIJKLS. Trong đó, điểm L cố định và LS = 40 m. Hỏi, khi đó cần dùng ít nhất bao nhiêu mát dây đèn led để trang trí (làm tròn đến hàng đơn vị?
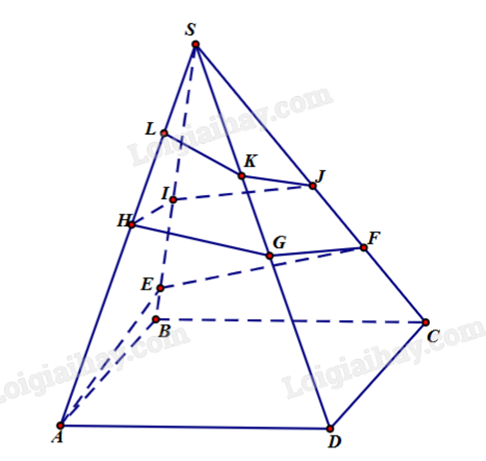
Đáp án:
Đáp án:
Sử dụng phương pháp trải đa diện và định lí cosin trong tam giác.
Cắt hình chóp theo cạnh bên SA rồi trải ra mặt phẳng hai lần, ta có hình vẽ sau:
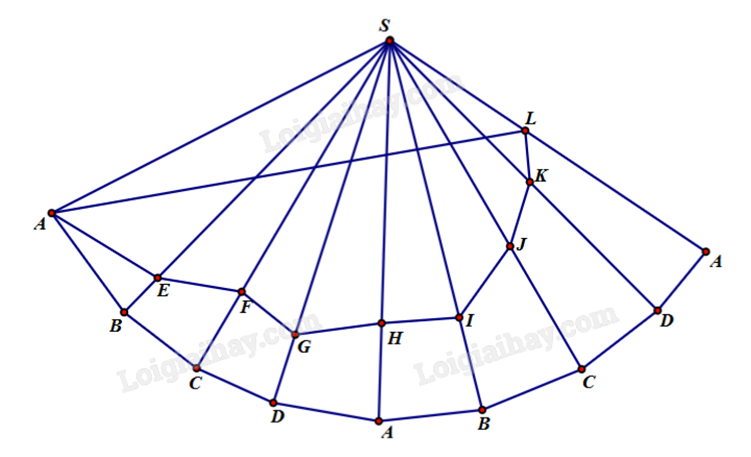
Từ đó suy ra chiều dài dây đèn led ngắn nhất bằng AL + LS.
Vì S.ABCD là hình chóp đều nên \(\widehat {ASL} = {8.15^o} = {120^o}\).
Sử dụng định lí cosin cho tam giác ASL, ta có:
\(A{L^2} = S{A^2} + S{L^2} - 2.SA.SL.\cos \widehat {ASL} = {200^2} + {40^2} - 2.200.40.\cos {120^o} = 49600\).
Suy ra \(AL = \sqrt {49600} = 40\sqrt {31} \).
Vậy chiều dài dây đèn led cần ít nhất là \(40\sqrt {31} + 40 \approx 263\) mét.

Các bài tập cùng chuyên đề
Trong Ví dụ 6, xác định giao điểm của đường thẳng DF và mặt phẳng (ABC).
Trong các hình chóp ở HĐ7, hình chóp nào có ít mặt nhất? Xác định số cạnh và số mặt của hình chóp đó.
Cho hình chóp S.ABCD. Gọi tên các mặt bên và mặt đáy của hình chóp đó.
Các hình ảnh dưới đây có đặc điểm chung nào với hình chóp tam giác đều mà em đã học ở lớp 8?

Hình 29 là hình ảnh của chặn giấy bằng gỗ có bốn mặt phân biệt là các tam giác. Vẽ hình biểu diễn của chặn giấy bằng gỗ đó.

Cho tứ diện ABCD. Các điểm M, N, P lần lượt thuộc các cạnh AB, AD, BC sao cho:
\(\frac{{AM}}{{AB}} = \frac{1}{3},\frac{{AN}}{{AD}} = \frac{2}{3},\frac{{BP}}{{BC}} = \frac{3}{4}\)
a) Xác định E. F lần lượt là giao điểm của các đường thẳng AC, BD với mặt phẳng (MNP)
b) Chứng minh rằng các đường thẳng NE, PE và CD cùng đi qua một điểm
Hình 25 là hình nhr của khối rubik tam giác (Pyramix). Quan sát Hình 25 và trả lời các câu hỏi:
a) Khối rubik tam giác có bao nhiêu đỉnh? Các đỉnh có cùng nằm trong một mặt phẳng không?
b) Khối rubik tam giác có bao nhiêu mặt? Mỗi mặt của khối rubik tam giác là những hình gì?

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và AD.
a) Xác định giao điểm của mặt phẳng (CMN) với các đường thẳng AB, SB
b) Xác định giao tuyến của mặt phẳng (CMN) với mỗi mặt phẳng (SAB) và (SBC)
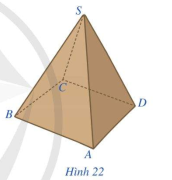
Hình 22 là hình ảnh của một hộp quà lưu niệm có dạng hình chóp tứ giác đều S.ABCD. Quan sát Hình 22 và trả lời các câu hỏi:
a) Đỉnh S có nằm trong mặt phẳng (ABCD) hay không?
b) Mỗi mặt của hộp quà lưu niệm có dạng hình gì?
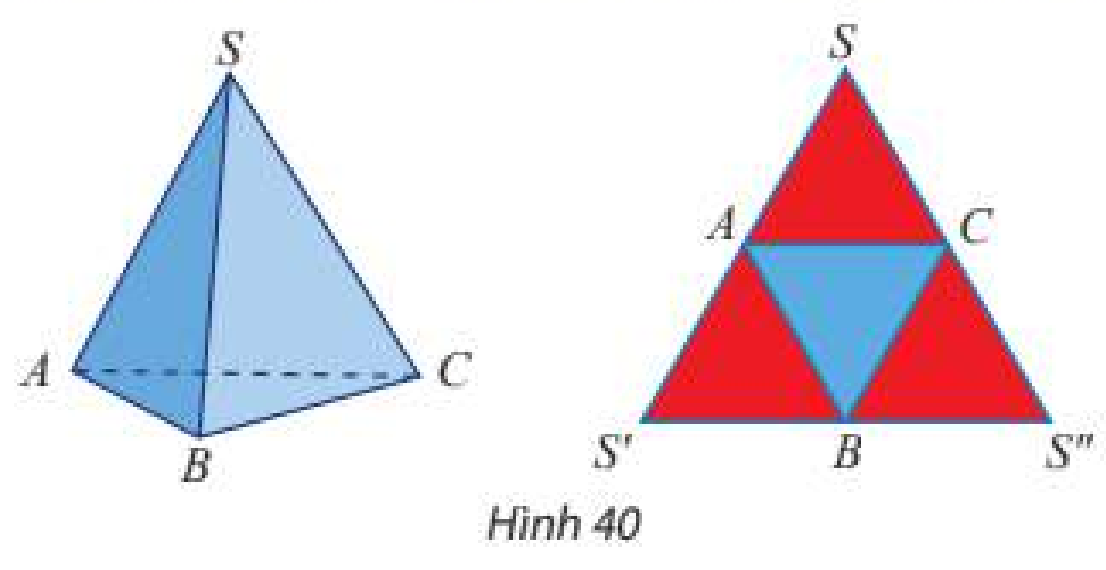
Nêu cách tạo lập tứ diện đều \(SABC\) từ tam giác đều \(SS'S''\) theo gợi ý ở Hình 40.
Cho hình chóp \(S.ABCD\). Trên các cạnh bên của hình chóp lấy lần lượt các điểm \(A',B',C',D'\). Cho biết \(AC\) cắt \(B{\rm{D}}\) tại \(O\), \(A'C'\) cắt \(B'{\rm{D'}}\) tại \(O'\), \(AB\) cắt \(DC\) tại \(E\) và \(A'B'\) cắt \(D'C'\) tại \(E'\) (Hình 39). Chứng minh rằng:
a) \(S,O',O\) thẳng hàng;
b) \(S,E',E\) thẳng hàng.

Cho tứ diện \(SABC\). Gọi \(H,K\) lần lượt là hai điểm trên hai cạnh \(SA\) và \(SC\left( {H \ne S,A;K \ne S,C} \right)\) sao cho \(HK\) không song song với \(AC\). Gọi \(I\) là trung điểm của \(BC\) (Hình 38).
a) Tìm giao điểm của đường thẳng \(HK\) và mặt phẳng \(\left( {ABC} \right)\).
b) Tìm giao tuyến của các mặt phẳng \(\left( {SAI} \right)\) và \(\left( {ABK} \right)\); \(\left( {SAI} \right)\) và \(\left( {BCH} \right)\).
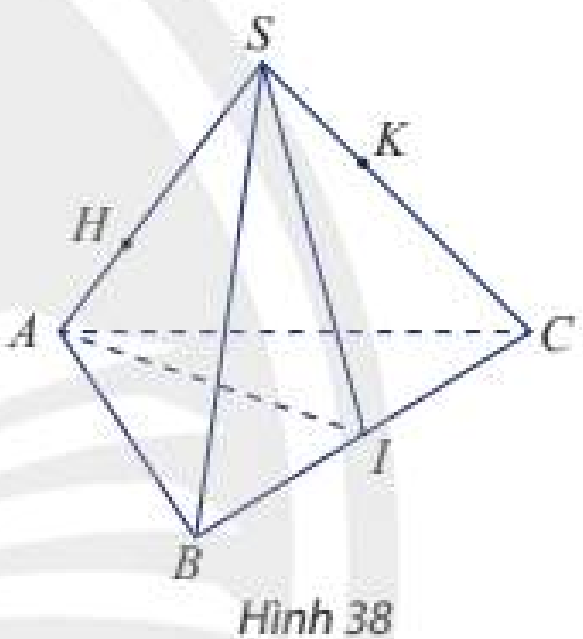
Trong Hình 34, hình chóp nào có số mặt ít nhất?
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?

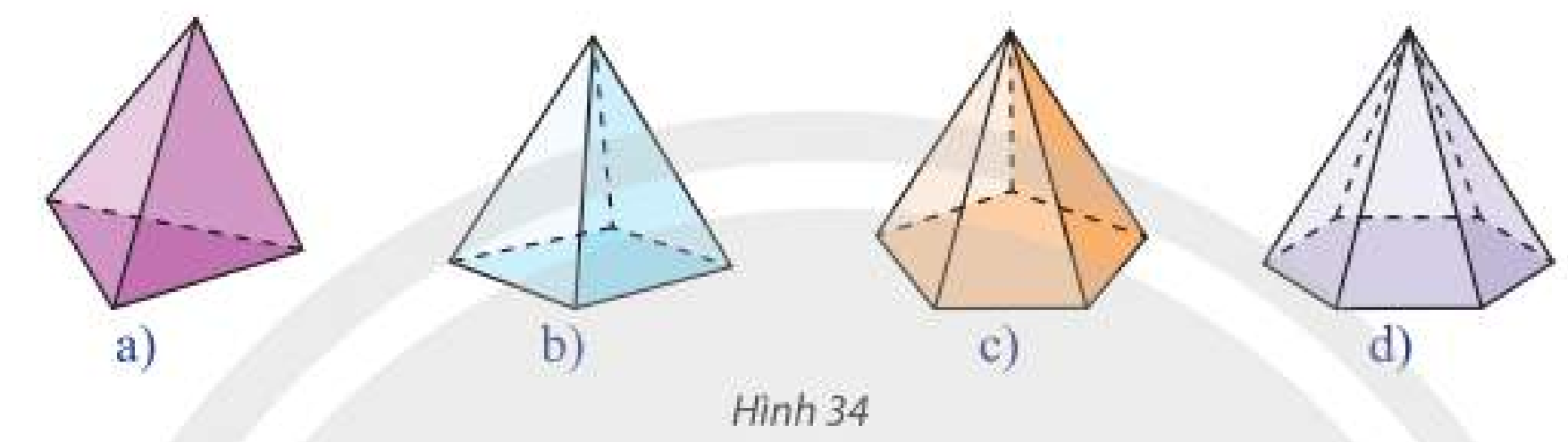
b) Tìm điểm giống nhau của các hình trong Hình 31.
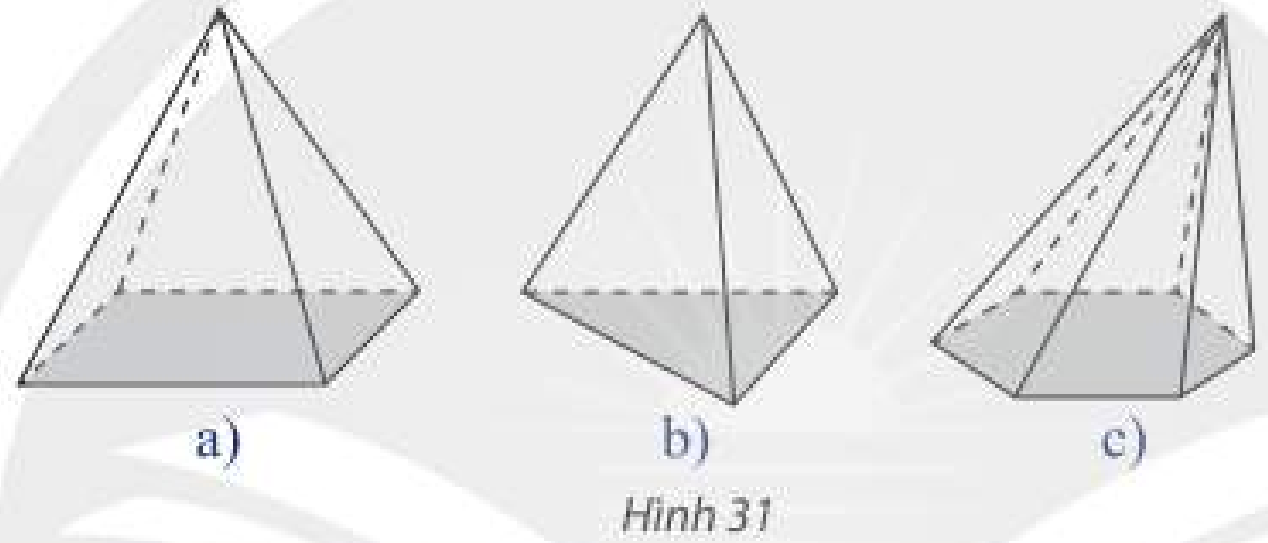
Trong các hình sau, hình nào có thể là hình biểu diễn một hình tứ diện?
-
A.
(I)
-
B.
(I), (II)
-
C.
(I), (II), (IV)
-
D.
(I), (II), (III), (IV)
Hình chóp lục giác có bao nhiêu mặt bên?
-
A.
4
-
B.
5
-
C.
6
-
D.
7
Hình chóp có 16 cạnh thì có bao nhiêu mặt?
-
A.
7
-
B.
8
-
C.
9
-
D.
10
Khẳng định nào sau đây là đúng về hình tứ diện đều?
-
A.
Mặt đáy là hình thoi
-
B.
Mặt đáy là hình vuông
-
C.
Mặt bên là tam giác cân
-
D.
Mặt bên luôn là tam giác đều
Khẳng định nào sau đây là đúng?
-
A.
Hình chóp tứ giác là một hình tứ diện
-
B.
Hình tứ diện đều có mặt đáy là tam giác đều
-
C.
Mặt bên của tứ diện đều là hình tam giác cân
-
D.
Cả A, B, C đều đúng
Một đồ vật trang trí có bốn mặt phân biệt là các tam giác (xem hình dưới đây). Vẽ hình hiểu diễn của đồ vật đó.
Cho bốn điểm \(A\), \(B\), \(C\), \(D\) không cùng thuộc một mặt phẳng. Khẳng định nào sau đây là SAI?
A. Bốn điểm \(A\), \(B\), \(C\), \(D\) đã cho đôi một khác nhau.
B. Không có ba điểm nào trong bốn điểm \(A\), \(B\), \(C\), \(D\) thẳng hàng.
C. Hai đường thẳng \(AC\) và \(BD\) song song với nhau.
D. Hai đường thẳng \(AC\) và \(BD\) không có điểm chung với nhau.
Cho tứ diện \(ABCD,\) vị trí tương đối của hai đường thẳng \(AC\) và \(BD\) là
-
A.
Cắt nhau.
-
B.
Song song.
-
C.
Chéo nhau.
-
D.
Trùng nhau.
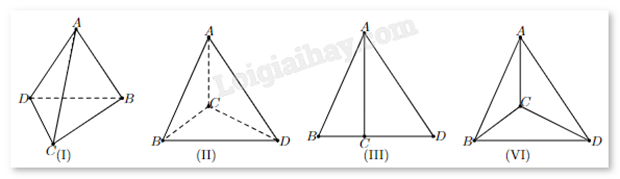
Có bao nhiêu hình biểu diễn cho hình tứ diện trong bốn hình dưới đây?
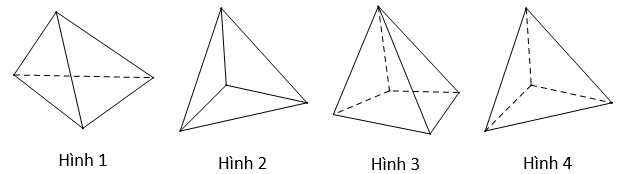
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là
-
A.
5 mặt, 5 cạnh.
-
B.
6 mặt, 5 cạnh.
-
C.
6 mặt, 10 cạnh.
-
D.
5 mặt, 10 cạnh.
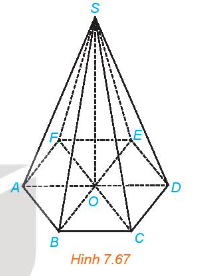
Cho hình chóp S.A1A2...An. Gọi O là hình chiếu của S trên mặt phẳng (A1A2...An).
a) Trong trường hợp hình chóp đã cho là đều, vị trí của điểm O có gì đặc biệt đối với đa giác đều A1A2...An?
b) Nếu đa giác A1A2...An là đều và O là tâm của đa giác đó thì hình chóp đã cho có gì đặc biệt?
Tháp lớn tại Bảo tàng Louvre ở Paris (H.7.66) (với kết cấu kính và kim loại) có dạng hình chóp với đây là hình vuông có cạnh bằng 34 m, các cạnh bên bằng nhau và có độ dài xấp xỉ 32,3 m (theo Wikipedia.org).
Giải thích vì sao hình chiếu của đỉnh trên đây là tâm của đáy tháp.

Cho biết kim tự tháp Khafre tại Ai Cập có dạng hình chóp tứ giác đều với chiều cao khoảng 136 m và cạnh đáy dài khoảng 152 m. Tính độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp.
(nguồn: https://vi.wikipedia.org/wiki/ Kim tự tháp_Khafre)

Cho hình chóp tứ giác đều \(S.ABCD\) có \(O\) là tâm của đáy và \(AB = a,SA = 2a\). Tính \(SO\) theo \(a\).
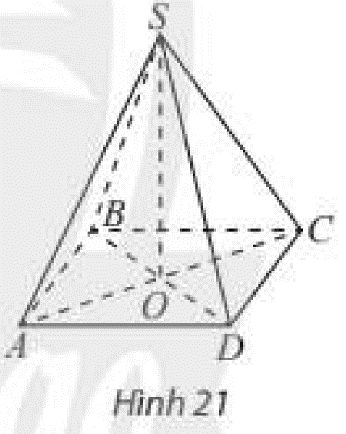
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông với tâm \(O\) và các cạnh bên của hình chóp bằng nhau (Hình 21). Đường thẳng \(SO\) có vuông góc với đáy không?
Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp.






