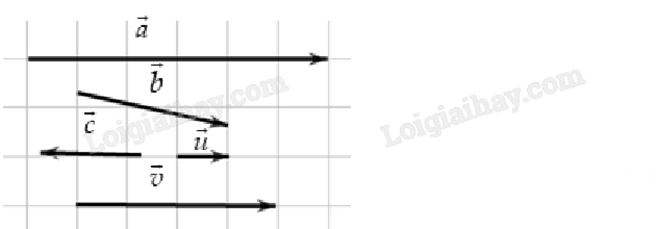
Cho các vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c ,\overrightarrow u \) và \(\overrightarrow v \) như trong hình dưới. Hỏi có bao nhiêu vecto cùng hướng với \(\overrightarrow u \)?
-
A.
4
-
B.
2
-
C.
3
-
D.
1
Quan sát hình vẽ. Các vecto cùng hướng có giá song song và cùng chiều nhau.
Các vecto cùng hướng với \(\overrightarrow u \) là \(\overrightarrow a \) và \(\overrightarrow v \).
Đáp án : B

Các bài tập cùng chuyên đề
Hai ca nô A và B chạy trên sông với các vận tốc riêng có cùng độ lớn là 15km/h. Tuy vậy, ca nô A chạy xuôi dòng còn ca nô B chạy ngược dòng. Vận tốc của dòng nước trên sông là 3 km/h.
a) Hãy thể hiện trên hình vẽ, vectơ vận tốc \(\overrightarrow v \) của dòng nước và các vectơ vận tốc thực tế \(\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \) của các ca nô A, B. ?
b) Trong các vectơ \(\overrightarrow v ,\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \), những cặp vectơ nào cùng phương và những cặp vectơ nào ngược hướng?
Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \)được gọi là cùng hướng, còn hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ \(\overrightarrow a \) và các vectơ ngược hướng với vectơ \(\overrightarrow a \).
Quan sát các làn đường trong Hình 4.5 và cho biết những nhận xét nào sau đây là đúng.
a) Các làn đường song song với nhau.
b) Các xe chạy theo cùng một hướng
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau.
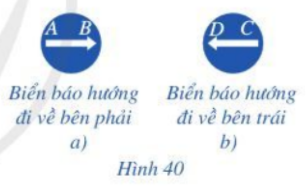
Quan sát hai biển báo ở Hình 40a, 40b, cho biết hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng hướng hay không.
Quan sát Hình 39 và cho biết vị trí tương đối giữa giá của vectơ \(\overrightarrow {CD} \) với giá của vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {PQ} \).
Cho A, B, C là ba điểm thẳng hàng, B nằm giữa A và C. Viết các cặp vectơ cùng hướng, ngược hướng trong những vectơ sau: \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BA} ,\overrightarrow {BC} ,\overrightarrow {CA} ,\overrightarrow {CB} .\)
Khẳng định sau đây đúng hay sai? Hãy giải thích.
Nếu 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)cùng hướng.
Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ \(\overrightarrow x \);
b) Cùng hướng với vectơ \(\overrightarrow a \) ;
Ngược hướng với vectơ \(\overrightarrow u \).
Bạn có nhận xét gì về giá của các cặp vectơ\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \) trong Hình 6?
Cho hình thang ABCD có hai cạnh đáy là AB và DC (hình 15). Điểm M nằm trên đoạn DC.
a) Gọi tên các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \)
b) Gọi tên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)
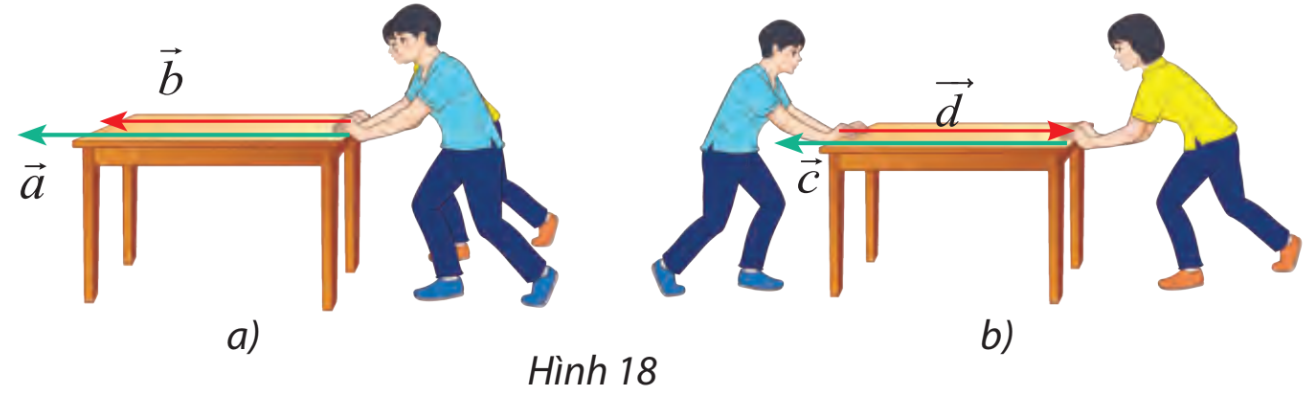
Tìm các lực cùng hướng và ngược hướng trong số các lực đẩy được biểu diễn bằng các vectơ trong hình 18
Cho tam giác \(ABC\). Gọi \(M\) là trung điểm của cạnh \(BC\) và \(G\) là trọng tâm của tam giác. Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?
a) Hai vectơ \(\overrightarrow {GA} \) và \(\overrightarrow {GM} \) cùng phương.
b) Hai vectơ \(\overrightarrow {GA} \) và \(\overrightarrow {GM} \) cùng hướng.
c) Hai vectơ \(\overrightarrow {GA} \) và \(\overrightarrow {GM} \) ngược hướng.
d) Độ dài của vectơ \(\overrightarrow {AM} \) bằng ba lần độ dài của vectơ \(\overrightarrow {MG} \).
Cho hình bình hành \(ABCD\) tâm \(O.\) Xét các vectơ có hai điểm mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D\) và \(O.\) Số các vectơ khác vectơ – không và cùng phương với \(\overrightarrow {AC} \) là:
A. 6
B. 3
C. 4
D. 2
Cho đoạn thẳng \(AC\) và \(B\) là một điểm nằm giữa \(A,\,\,C.\) Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?
A. Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \) cùng hướng.
B. Hai vectơ \(\overrightarrow {CA} \) và \(\overrightarrow {BC} \) cùng hướng.
C. Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng.
D. Hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BA} \) cùng hướng.
Trong mặt phẳng cho hai điểm phân biệt A, B. Tập hợp tất cả các điểm M thỏa mãn \(\overrightarrow {AM} \) ngược hướng với \(\overrightarrow {AB} \) là hình gì?
A. Đường thẳng AB
B. Tia AB
C. Tia đối của tia AB trừ điểm A
D. Đoạn thẳng AB
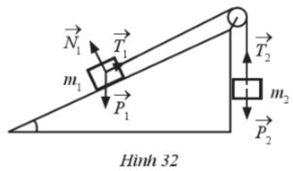
Trong mặt phẳng nghiêng không có ma sát, cho hệ vật m1, m2, hai vật nối với nhau bằng một sợi dây không dãn vắt qua ròng rọc (Hình 32). Giả sử bỏ qua khối lượng của dây và ma sát của ròng rọc.
a) Tìm các cặp vectơ cùng phương trong các vectơ ở Hình 32.
b) Những cặp vectơ cùng phương đó có cùng hướng không?
Cho đoạn thẳng AB và điểm C nằm giữa hai điểm A, B. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AC} = \frac{{AC}}{{AB}}\overrightarrow {AB} \)
B. \(\overrightarrow {AC} = - \frac{{AC}}{{AB}}\overrightarrow {AB} \)
C. \(\overrightarrow {AC} = \frac{{AB}}{{AC}}\overrightarrow {AB} \)
D. \(\overrightarrow {AC} = - \frac{{AB}}{{AC}}\overrightarrow {AB} \)
Cho đoạn thẳng BC và điểm A nằm giữa hai điểm B, C. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AC} = \frac{{AC}}{{AB}}\overrightarrow {AB} \)
B. \(\overrightarrow {AC} = - \frac{{AC}}{{AB}}\overrightarrow {AB} \)
C. \(\overrightarrow {AC} = \frac{{AB}}{{AC}}\overrightarrow {AB} \)
D. \(\overrightarrow {AC} = - \frac{{AB}}{{AC}}\overrightarrow {AB} \)
Cho hình thang ABCD với hai đáy là AB, CD và có hai đường chéo cắt nhau tại O
a) Gọi tên hai vectơ cùng hướng với \(\overrightarrow {AO} \)
b) Gọi tên hai vectơ ngược hướng với \(\overrightarrow {AB} \)
Cho tam giác ABC. Đặt \(\overrightarrow a = \overrightarrow {AB} ;\overrightarrow b = \overrightarrow {AC} \). Các cặp vectơ nào sau đây cùng phương?
A. \(2\overrightarrow a + \overrightarrow b \) và \(\overrightarrow a + 2\overrightarrow b \)
B. \(\overrightarrow a - 2\overrightarrow b \) và \(2\overrightarrow a - \overrightarrow b \)
C. \(5\overrightarrow a + \overrightarrow b \) và \( - 10\overrightarrow a - 2\overrightarrow b \)
D. \(\overrightarrow a + \overrightarrow b \) và \(\overrightarrow a - \overrightarrow b \)
Cho ba điểm A, B, C phân biệt thẳng hàng. Trong trường hợp nào thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
a) Cùng hướng? b) Ngược hướng?
Cho ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) cùng phương. Chứng tỏ rằng có ít nhất hai vectơ cùng hướng trong ba vectơ đó.
Trên trục \(\left( {O;\overrightarrow e } \right)\) cho các điểm A ,B, C, D có tọa độ lần lượt là 4; -1; -5; 0.
a) Vẽ trục và biểu diễn các điểm đã cho lên trên trục đó.
b) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng hay ngược hướng?
Chứng minh khẳng định sau: Hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương khi và chỉ khi có một số thực k sao cho \({x_1}{\rm{ = }}k{x_2}\) và \({y_1} = {\rm{ }}k{y_2}\) .
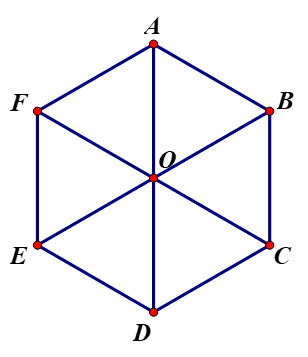
Cho lục giác đều ABCDEF tâm O như hình vẽ bên. Vectơ \(\overrightarrow {OB} \) cùng phương với vectơ nào sau đây?
-
A.
\(\overrightarrow {OC} \)
-
B.
\(\overrightarrow {BC} \)
-
C.
\(\overrightarrow {BE} \)
-
D.
\(\overrightarrow {OA} \)
Cho hình bình hành ABCD. Vecto nào sau đây cùng phương với \(\overrightarrow {AB} \)?
-
A.
\(\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {DC} \)
-
B.
\(\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {DA} \)
-
C.
\(\overrightarrow {AD} ,\overrightarrow {CD} ,\overrightarrow {DC} \)
-
D.
\(\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {CB} \)
Cho vectơ \(\overrightarrow a = \left( {2;2} \right)\). Hãy tìm tọa độ một vectơ đơn vị \(\overrightarrow e \) cùng hướng với vectơ \(\overrightarrow a \).
Cho tam giác ABC đều. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Cặp vectơ nào sau đây cùng hướng?
-
A.
$\overset{\rightarrow}{MA}$ và $\overset{\rightarrow}{MB}$.
-
B.
$\overset{\rightarrow}{MN}$ và $\overset{\rightarrow}{CB}$.
-
C.
$\overset{\rightarrow}{AB}$ và $\overset{\rightarrow}{MB}$.
-
D.
$\overset{\rightarrow}{AN}$ và $\overset{\rightarrow}{CA}$.
Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ $\overset{\rightarrow}{a},\overset{\rightarrow}{b},\overset{\rightarrow}{c}$ (hình vẽ). Chọn khẳng định sai trong các khẳng định sau.

-
A.
$\overset{\rightarrow}{c}$ và $\overset{\rightarrow}{b}$ là hai vectơ cùng phương.
-
B.
$\overset{\rightarrow}{c}$ và $\overset{\rightarrow}{b}$ là hai vectơ cùng hướng.
-
C.
$\overset{\rightarrow}{a}$ và $\overset{\rightarrow}{c}$ là hai vectơ cùng hướng.
-
D.
$\overset{\rightarrow}{a}$ và $\overset{\rightarrow}{b}$ là hai vectơ cùng phương.