Giải các bất phương trình sau:
a) \({4^x} < 2\sqrt 2 \);
b) \({\left( {\frac{1}{{\sqrt 3 }}} \right)^{x - 1}} \ge \frac{1}{9}\);
c) \(5.{\left( {\frac{1}{2}} \right)^x} < 40\);
d) \({4^{2x}} < {8^{x - 1}}\);
e) \({\left( {\frac{1}{5}} \right)^{2 - x}} \le {\left( {\frac{1}{{25}}} \right)^x}\);
g) \(0,{25^{x - 2}} > 0,{5^{x + 1}}\).
Sử dụng kiến thức về giải bất phương trình chứa mũ để giải bất phương trình:
Bảng tổng kết về nghiệm của các bất phương trình:
|
Bất phương trình |
\(b \le 0\) |
\(b > 0\) |
|
|
\(a > 1\) |
\(0 < a < 1\) |
||
|
\({a^x} > b\) |
\(\forall x \in \mathbb{R}\) |
\(x > {\log _a}b\) |
\(x < {\log _a}b\) |
|
\({a^x} \ge b\) |
\(x \ge {\log _a}b\) |
\(x \le {\log _a}b\) |
|
|
\({a^x} < b\) |
Vô nghiệm |
\(x < {\log _a}b\) |
\(x > {\log _a}b\) |
|
\({a^x} \le b\) |
\(x \le {\log _a}b\) |
\(x \ge {\log _a}b\) |
|
Chú ý:
+ Nếu \(a > 1\) thì \({a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) > v\left( x \right)\)
+ Nếu \(0 < a < 1\) thì \({a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) < v\left( x \right)\)
a) \({4^x} < 2\sqrt 2 \) \( \Leftrightarrow {\left( {\sqrt 2 } \right)^{4x}} < {\left( {\sqrt 2 } \right)^3} \) \( \Leftrightarrow 4x < 3\left( {do\;\sqrt 2 > 1} \right) \) \( \Leftrightarrow x < \frac{3}{4}\)
Vậy bất phương trình có nghiệm \(x < \frac{3}{4}\).
b) \({\left( {\frac{1}{{\sqrt 3 }}} \right)^{x - 1}} \ge \frac{1}{9} \) \( \Leftrightarrow {\left( {\frac{1}{3}} \right)^{\frac{{x - 1}}{2}}} \ge {\left( {\frac{1}{3}} \right)^2} \) \( \Leftrightarrow \frac{{x - 1}}{2} \le 2\left( {do\,0 < \frac{1}{3} < 1} \right) \) \( \Leftrightarrow x - 1 \le 4 \) \( \Leftrightarrow x \le 5\)
Vậy bất phương trình có nghiệm \(x \le 5\).
c) \(5.{\left( {\frac{1}{2}} \right)^x} < 40 \) \( \Leftrightarrow {\left( {\frac{1}{2}} \right)^x} < 8 \) \( \Leftrightarrow {2^{ - x}} < {2^3} \) \( \Leftrightarrow - x < 3\left( {do\;2 > 1} \right) \) \( \Leftrightarrow x > - 3\)
Vậy bất phương trình có nghiệm \(x > - 3\).
d) \({4^{2x}} < {8^{x - 1}} \) \( \Leftrightarrow {2^{4x}} < {2^{3\left( {x - 1} \right)}} \) \( \Leftrightarrow 4x < 3x - 3\left( {do\;2 > 1} \right) \) \( \Leftrightarrow x < - 3\)
Vậy bất phương trình có nghiệm \(x < - 3\).
e) \({\left( {\frac{1}{5}} \right)^{2 - x}} \le {\left( {\frac{1}{{25}}} \right)^x} \) \( \Leftrightarrow {5^{x - 2}} \le {5^{ - 2x}} \) \( \Leftrightarrow x - 2 \le - 2x\left( {do\;5 > 1} \right) \) \( \Leftrightarrow 3x \le 2 \) \( \Leftrightarrow x \le \frac{2}{3}\)
Vậy bất phương trình có nghiệm \(x \le \frac{2}{3}\).
g) \(0,{25^{x - 2}} > 0,{5^{x + 1}} \) \( \Leftrightarrow 0,{5^{2x - 4}} > 0,{5^{x + 1}} \) \( \Leftrightarrow 2x - 4 < x + 1\left( {do\;0,5 < 1} \right) \) \( \Leftrightarrow x < 5\)
Vậy bất phương trình có nghiệm \(x < 5\).

Các bài tập cùng chuyên đề
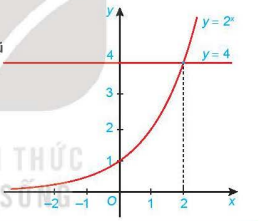
Cho đồ thị của hàm số \(y = {2^x}\) và \(y = 4\) như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình \({2^x} > 4.\)
Bác Minh gửi tiết kiệm 500 triệu đồng ở một ngân hàng với lãi suất không đổi 7,5% một năm theo thể thức lãi kép kì hạn 12 tháng. Tổng số tiền bác Minh thu được (cả vốn lẫn lãi) sau n năm là:
\(A = 500.{\left( {1 + 0,075} \right)^n}\) (triệu đồng).
Tính thời gian tối thiểu gửi tiết kiệm để bác Minh thu được ít nhất 800 triệu đồng (cả vốn lẫn lãi).
Số lượng vi khuẩn ban đầu trong một mẻ nuôi cấy là 500 con. Người ta lấy một mẫu vi khuẩn trong mẻ nuôi cấy đó, đếm số lượng vi khuẩn và thấy rằng tỉ lệ tăng trưởng vi khuẩn là 40% mỗi giờ. Khi đó số lượng vi khuẩn N(t) sau t giờ nuôi cấy được ước tính bằng công thức sau:
\(N\left( t \right) = 500{e^{0,4t}}.\)
Hỏi sau bao nhiêu giờ nuôi cấy, số lượng vi khuẩn vượt mức 80 000 con?
Giải các bất phương trình sau:
a) \({2^x} > 16\);
b) \(0,{1^x} \le 0,001\);
c) \({\left( {\frac{1}{5}} \right)^{x - 2}} \ge {\left( {\frac{1}{{25}}} \right)^x}\).
Xét quần thể vi khuẩn ở Hoạt động 1.
a) Ở những thời điểm nào thì số lượng cá thể vi khuẩn vượt quá 50000?
b) Ở những thời điểm nào thì số lượng cá thể vi khuẩn vượt quá 50000 nhưng chưa vượt quá 100000?
Giải các bất phương trình sau:
a) \({\left( {\frac{1}{3}} \right)^{2{\rm{x}} + 1}} \le 9\);
b) \({4^x} > {2^{x - 2}}\).
Tập nghiệm của bất phương trình \(0,{5^{3{\rm{x}} - 1}} > 0,25\) là
A. \(\left( { - \infty ;1} \right)\).
B. \(\left( {1; + \infty } \right)\).
C. \(\left( {0;1} \right)\).
D. \(\left( { - \infty ; - \frac{1}{3}} \right)\).
Giải mỗi bất phương trình sau:
a) \({7^{x + 3}} < 343\)
b) \({\left( {\frac{1}{4}} \right)^x} \ge 3\)
Cho hai ví dụ về bất phương trình mũ cơ bản.
Tập nghiệm của bất phương trình \({(0,2)^x} > 1\) là:
A. \(\left( { - \infty ;0,2} \right)\)
B. \(\left( {0,2; + \infty } \right)\)
C. \(\left( {0; + \infty } \right)\)
D. \(\left( { - \infty ;0} \right)\)
Tập nghiệm của bất phương trình \({\log _{\frac{1}{4}}}x > - 2\) là:
A. \(\left( { - \infty ;16} \right)\)
B. \(\left( {16; + \infty } \right)\)
C. \((0;16)\)
D. \(\left( { - \infty ;0} \right)\)
Giải các bất phương trình mũ sau:
a) \({2^{2x - 3}} > \frac{1}{4}\)
b) \({\left( {\frac{1}{2}} \right)^{{x^2}}} \ge {\left( {\frac{1}{2}} \right)^{5x - 6}}\);
c) \({25^x} \le {5^{4x - 3}}\);
d) \({9^x} - {3^x} - 6 \le 0\).
Với giá trị nào của \(x\) thì đồ thị hàm số \(y = {\left( {\frac{2}{3}} \right)^x}\) nằm phía trên đường thẳng \(y = 1\)?
A. \(x > 0\).
B. \(x < 0\).
C. \(x > 1\).
D. \(x < 1\).
Nghiệm của bất phương trình \({2^x} < 5\) là:
A. \(x > {\log _2}5.\)
B. \(x < {\log _5}2.\)
C. \(x < {\log _2}5.\)
D. \(x > {\log _5}2.\)
Giải mỗi bất phương trình sau:
a) \({\left( {0,2} \right)^{2x + 1}} > 1;\)
b) \({27^{2x}} \le \frac{1}{9};\)
c) \({\left( {\frac{1}{2}} \right)^{{x^2} - 5x + 4}} \ge 4;\)
d) \({\left( {\frac{1}{{25}}} \right)^{x + 1}} < {125^{2x}};\)
e) \({\left( {\sqrt 2 - 1} \right)^{3x - 2}} < {\left( {\sqrt 2 + 1} \right)^{4 - x}};\)
g) \({\left( {0,5} \right)^{2{x^2} - x}} > {\left( {\sqrt 2 } \right)^{4x - 12}}.\)
Tập nghiệm của bất phương trình \({2^{\sqrt x }} > 1\) là:
A. \(\left( {0; + \infty } \right).\)
B. \(\left[ {0; + \infty } \right).\)
C. \(\mathbb{R}.\)
D. \(\mathbb{R}\backslash \left\{ 0 \right\}.\)
Tập nghiệm của bất phương trình \(0,{3^{3x - 1}} > 0,09\) là
A. \(\left( {1; + \infty } \right)\)
B. \(\left( { - \infty ;1} \right)\)
C. \(\left( { - \infty ; - \frac{1}{3}} \right)\)
D. \(\left( {0;1} \right)\)
Tập nghiệm của bất phương trình \({\left( {\frac{1}{2}} \right)^{2{x^2} - x + 1}} \le {\left( {\frac{1}{4}} \right)^x}\) là
A. \(\left[ {\frac{1}{2};1} \right]\).
B. \(\left( { - \infty ;\frac{1}{2}} \right] \cup \left[ {1; + \infty } \right)\).
C. \(\left( {\frac{1}{2};1} \right)\).
D. \(\left( { - \infty ;\frac{1}{2}} \right) \cup \left( {1; + \infty } \right)\).
Tập nghiệm của bất phương trình \({2^x} \le 4\) là
-
A.
\(( - \infty ;2]\)
-
B.
\([0;2]\)
-
C.
\(( - \infty ;2)\)
-
D.
\((0;2)\)
Tập nghiệm của bất phương trình \({\left( {\frac{1}{2}} \right)^x} < \frac{1}{8}\) là?
-
A.
\((3; + \infty )\)
-
B.
\(( - \infty ;3)\)
-
C.
\([3; + \infty )\)
-
D.
\(( - \infty ;3]\)
Tập nghiệm của bất phương trình \({(0,21)^x} < 1\) là
-
A.
\(( - \infty ;0]\)
-
B.
\([0; + \infty )\)
-
C.
\(( - \infty ;0)\)
-
D.
\((0; + \infty )\)
Tập nghiệm của bất phương trình \({5^{x - 1}} \ge {5^{{x^2} - x - 9}}\) là
-
A.
[-4;2]
-
B.
\(( - \infty ; - 4] \cup [2; + \infty )\)
-
C.
[-2;4]
-
D.
\(( - \infty ; - 2] \cup [4; + \infty )\)
Tập nghiệm S của bất phương trình \({5^{x + 2}} < {\left( {\frac{1}{{125}}} \right)^{ - x}}\) là
-
A.
\(S = \left( { - \infty ;1} \right)\)
-
B.
\(S = \left( { - \infty ;2} \right)\)
-
C.
\(S = \left( {2; + \infty } \right)\)
-
D.
\(S = \left( {1; + \infty } \right)\)
Bất phương trình \({9^{x + 1}} > {27^{2x + 1}}\) tương đương với
-
A.
\(x < 1\)
-
B.
\(x - 1 > 0\)
-
C.
\(x < - \frac{1}{4}\)
-
D.
\(x \ne 0\)
Tập nghiệm của bất phương trình \({\left( {\frac{1}{3}} \right)^x} > 9\) là
-
A.
\(\left( {2;\, + \infty } \right)\)
-
B.
\(\left( { - \infty ;\, - 2} \right)\)
-
C.
\(\left( { - 2;\, + \infty } \right)\)
-
D.
\(\left( { - 2;\,0} \right)\)
Bất phương trình \({\left( {\frac{1}{2}} \right)^{{x^2} - 3x}} \ge 1\) có tất cả bao nhiêu nghiệm nguyên?
-
A.
2
-
B.
3
-
C.
4
-
D.
1
Ta coi năm lấy làm mốc để tính dân số của một vùng (hoặc một quốc gia) là năm 0. Khi đó, dân số của quốc gia đó ở năm thứ t là hàm số theo biến t được cho bởi công thức \(S = A.{e^{r.t}}\). Trong đó A là dân số của vùng (hoặc quốc gia) đó ở năm 0 và r là tỉ lệ tăng dân số hàng năm. Biết rằng dân số Việt Nam năm 2021 ước tính là 98 564 407 người và tỉ lệ tăng dân số hằng năm là 0,93%. Hỏi từ năm nào trở đi, dân số nước ta vượt 120 triệu người?
Tập nghiệm của bất phương trình $\left(\frac{1}{2}\right)^{x^{2}+4x}>\frac{1}{32}$ là
-
A.
$\{-5;1\}$.
-
B.
$(1;+\infty)$.
-
C.
$(-5;1)$.
-
D.
$(-\infty;-5)\cup(1;+\infty)$.






