a) Vẽ đồ thị hàm số \(y = {3^x}\) và đường thẳng y = 7.
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({3^x} = 7\).
Dựa vào kiến thức đã học ở bài trước để vẽ đồ thị.
a) Ta có bảng sau:

Ta có đồ thị sau:
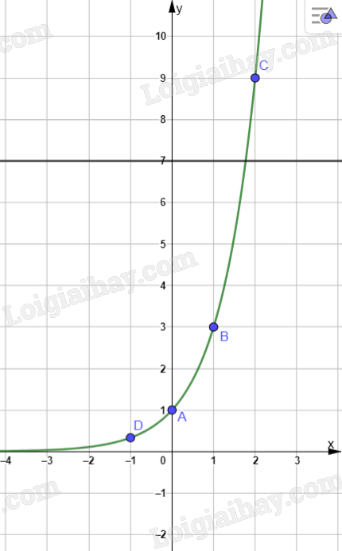
b) Hai đồ thị \(y = {3^x}\) và y = 7 có 1 giao điểm. Vậy số nghiệm của phương trình \({3^x} = 7\) là 1.

Các bài tập cùng chuyên đề
Giải các phương trình sau:
a) \({2^{3x-1}} = \frac{1}{{{2^{x + 1}}}};\)
b) \(2{e^{2x}} = 5.\)
Xét phương trình: \({2^{x + 1}} = \frac{1}{4}.\)
a) Khi viết \(\frac{1}{4}\) thành lũy thừa của 2 thì phương trình trên trở thành phương trình nào?
b) So sánh số mũ của 2 ở hai vế của phương trình nhận được ở câu a để tìm x.
Giải các phương trình sau:
a) \({3^{x - 1}} = 27;\)
b) \({100^{2{x^2} - 3}} = 0,{1^{2{x^2} - 18}};\)
c) \(\sqrt 3 {e^{3x}} = 1;\)
d) \({5^x} = {3^{2x - 1}}.\)
Giả sử nhiệt độ \(T\left( {^0C} \right)\) của một vật giảm dần theo thời gian cho bởi công thức: \(T = 25 + 70{e^{ - 0,5t}},\) trong đó thời gian t được tính bằng phút.
a) Tìm nhiệt độ ban đầu của vật.
b) Sau bao lâu nhiệt độ của vật còn lại \({30^o}C\)?
Công thức tính khối lượng còn lại của một chất phóng xạ từ khối lượng ban đầu \({M_0}\) là \(M\left( t \right) = {M_0}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\), trong đó \(t\) là thời gian tính từ thời điểm ban đầu và \(T\) là chu kì bán rã của chất. Đồng vị plutonium-234 có chu kì bản rã là 9 giờ.
(Nguồn: https://pubchem.ncbi.nlm.nih.gov/element/Plutonium#section=Atomic- Mass-Half-Life-and-Decay)
Từ khối lượng ban đầu 200 g, sau bao lâu thì sau bao lâu thì khối lượng plutonium-234 còn lại là:
a) 100 g?
b) 50 g?
c) 20 g?
Giải các phương trình sau:
a) \({3^{x + 2}} = \sqrt[3]{9}\); b) \({2.10^{2{\rm{x}}}} = 30\); c) \({4^{2{\rm{x}}}} = {8^{2{\rm{x}} - 1}}\).
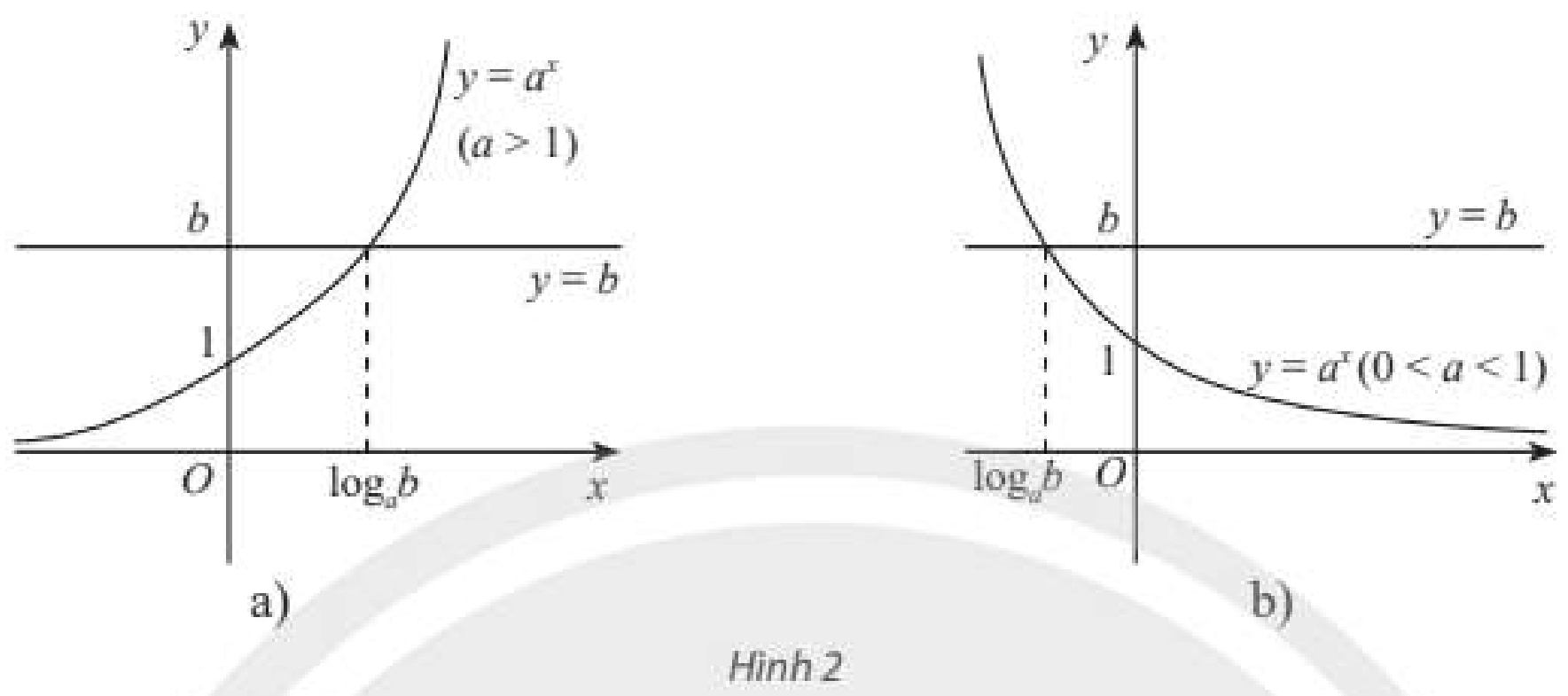
Cho đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) như Hình 2a (với \(a > 0\)) hay Hình 2b (với \(0 < a < 1\)). Từ đây, hãy nhận xét về số nghiệm và công thức nghiệm của phương trình \({a^x} = b\) trong hai trường hợp \(b > 0\) và \(b \le 0\).
Số lượng cá thể vi khuẩn của một mẻ nuôi cấy tuân theo công thức \(P\left( t \right) = {50.10^{kt}}\), trong đó \(t\) là thời gian tính bằng giờ kể từ thời điểm bắt đầu nuôi cấy, \(k\) là hằng số.
(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, năm 2017, trang 101)
a) Ban đầu mẻ có bao nhiêu cá thể vi khuẩn?
b) Sau 1 giờ thì mẻ có 100 cá thể vi khuẩn. Tìm giá trị của \(k\) (làm tròn kết quả đến hàng phần mười).
c) Sau bao lâu thì số lượng cá thể vi khuẩn đạt đến 50000?
Giải các phương trình sau:
a) \({5^{2x - 1}} = 25\);
b) \({3^{x + 1}} = {9^{2x + 1}}\);
c) \({10^{1 - 2x}} = 100000\).
Giải các phương trình sau. Làm tròn kết quả đến hàng phần nghìn.
a) \({3^{x + 2}} = 7\);
b) \({3.10^{2x + 1}} = 5\).
Phương trình \(0,{1^{2{\rm{x}} - 1}} = 100\) có nghiệm là:
A. \( - \frac{1}{2}\).
B. \(\frac{1}{3}\).
C. \(1\frac{1}{2}\).
D. \(2\frac{1}{3}\).
Chỉ số hay độ pH của một dung dịch được tính theo công thức: \(pH = - \log [{H^ + }]\) (Trong đó \([{H^ + }]\) chỉ nống độ hydrogen). Đo chỉ số pH của một mẫu nước sông, ta có kết quả là pH = 6,1.
a) Viết phương trình thể hiện nồng độ x của ion hydrogen \([{H^ + }]\) trong mẫu nước sông đó.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?
Giải mỗi phương trình sau:
a) \({9^{16 - x}} = {27^{x + 4}}\).
b) \({16^{x - 2}} = 0,{25.2^{ - x + 4}}\).
Cho hai ví dụ về phương trình mũ.
Nghiệm của phương trình \({3^{2x - 5}} = 27\) là
A. 1
B. 4
C. 6
D. 7
Giải các phương trình mũ sau:
a) \({4^{2x - 1}} = {8^{x + 3}}\);
b) \({9^{2x}} \cdot {27^{{x^2}}} = \frac{1}{3}\)
c) \({\left( {{e^4}} \right)^x} \cdot {e^{{x^2}}} = {e^{12}}\)
d) \({5^{2x - 1}} = 20\).
Áp suất khí quyển \(p\) lên một vật giảm khi độ cao tăng dần. Giả sử áp suất này (tính bằng milimét thuỷ ngân) được biểu diễn theo độ cao \(h\) (tính bằng kilômét) so với mực nước biển bằng công thức \(p\left( h \right) = 760 \cdot {e^{ - 0.145h}}\).
a) Một máy bay đang chịu áp suất khí quyển \(320{\rm{mmHg}}\). Tìm độ cao của máy bay đó.
b) Một người đứng trên đỉnh của một ngọn núi và chịu áp suất khí quyển \(667{\rm{mmHg}}\). Tìm chiều cao của ngọn núi này.
Giả sử giá trị còn lại \(V\) (triệu đồng) của một chiếc ô tô nào đó sau \(t\) năm được cho bằng công thức \(V\left( t \right) = 730 \cdot {(0,82)^t}\).
a) Theo mô hình này, khi nào chiếc xe có giá trị 500 triệu đồng?
b) Theo mô hình này, khi nào chiếc xe có giá trị 200 triệu đồng? (Kết quả của câu a và câu b được tính tròn năm).
Tập nghiệm của phương trình \({8^{2x - 1}} = {\left( {\frac{1}{4}} \right)^x}\) là
A. \(\left\{ {\frac{3}{8}} \right\}\).
B. \(\left\{ {\frac{2}{5}} \right\}\).
C. \(\left\{ {\frac{3}{4}} \right\}\).
D. \(\left\{ {\frac{2}{3}} \right\}\).
Nghiệm của bất phương trình \({\left( {\frac{1}{2}} \right)^x} \ge {\left( {\frac{1}{4}} \right)^2}\) là
A. \(x \ge 2\).
B. \(x \le 2\).
C. \(x \ge 4\).
D. \(x \le 4\).
Công thức tính khối lượng còn lại của một chất phóng xạ từ khối lượng ban đầu \({m_0}\) được cho bởi công thức: \(m\left( t \right) = {m_0}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}.\)
trong đó t là thời gian tính từ thời điểm ban đầu và \(T\) là chu kì bán rã của chất đó. Biết rằng chất phóng xạ polonium-210 có chu kì bán rã là 138 ngày. Từ khối lượng polonium-210 ban đầu \(100{\rm{\;g}}\), sau bao lâu khối lượng còn lại là:
a) \(50{\rm{\;g}}\)?
b) \(10{\rm{\;g}}\)?
(Kết quả tính theo ngày và làm tròn đến chữ số thập phân thứ hai).
Nghiệm của phương trình \({2^{x - 1}} = 8\) là:
A. \(2.\)
B. \(4.\)
C. \(3.\)
D. \(5.\)
Nghiệm của phương trình \({2^x} = 5\) là:
A. \(x = \sqrt 5 .\)
B. \(x = \frac{5}{2}.\)
C. \(x = {\log _2}5.\)
D. \(x = {\log _5}2.\)
Nghiệm của phương trình \({9^{2x + 1}} = {27^{x - 3}}\) là:
A. \(x = - 9.\)
B. \(x = 11.\)
C. \(x = 9.\)
D. \(x = - 11.\)
Giải mỗi phương trình sau:
a) \({3^{x - 1}} = 5;\)
b) \({3^{{x^2} - 4x + 5}} = 9;\)
c) \({2^{2x + 3}} = 8\sqrt 2 ;\)
d) \({8^{x - 2}} = {4^{1 - 2x}};\)
e) \({2^{{x^2} - 3x - 2}} = 0,{25.16^{x - 3}};\)
g) \({2^{{x^2} - 4x + 4}} = 3.\)
Người ta nuôi cấy vi khuẩn Bacillus subtilis trong nồi lên men và thu được số liệu sau: Lúc ban đầu, số tế bào/1 ml dịch nuôi là \({2.10^2}\). Sau 13 giờ, số tế bào/1 ml dịch nuôi là \(3,{33.10^9}\). Biết vi khuẩn Bacillus subtilis sinh trưởng trong điều kiện hoàn toàn tối ưu và sinh sản theo hình thức tự nhân đôi. Hỏi sau bao nhiêu phút, vi khuẩn Bacillus subtilis tự nhân đôi một lần (làm tròn kết quả đến hàng đơn vị)?
Dân số thành phố Hà Nội năm 2022 khoảng 8,4 triệu người. Giả sử tỉ lệ tăng dân số hàng năm của Hà Nội không đổi và bằng \(r = 1,04\% .\) Biết rằng, sau \(t\) năm dân số Hà Nội (tính từ mốc năm 2022) ước tính theo công thức: \(S = A.{e^{rt}},\)trong đó \(A\) là dân số năm lấy làm mốc. Hỏi từ năm nào trở đi, dân số của Hà Nội vượt quá 10 triệu người?
Nghiệm của phương trình \({3^{x - 1}} = 1\) là:
A. \(x = 1.\)
B. \(x = 0.\)
C. \(x = 2.\)
D. \(x = - 1.\)
Nghiệm của phương trình \(0,{5^x} = {\left( {\sqrt 2 } \right)^{x + 3}}\) là:
A. \(x = 3.\)
B. \(x = 1.\)
C. \(x = - 3.\)
D. \(x = - 1.\)
Giải các phương trình sau:
a) \({3^{2x + 1}} = \frac{1}{{27}}\);
b) \({5^{2x}} = 10\);
c) \({3^x} = 18\);
d) \(0,{2^{x - 1}} = \frac{1}{{\sqrt {125} }}\);
e) \({5^{3x}} = {25^{x - 2}}\);
g) \({\left( {\frac{1}{8}} \right)^{x + 1}} = {\left( {\frac{1}{{32}}} \right)^{x - 1}}\).






