Hình 5.25 là hình ảnh Cầu Cổng Vàng (The Golden Gate Bridge) ở Mỹ. Xét hệ trục tọa độ Oxyz với O là bệ của chân cột trụ tại mặt nước, trục Oz trùng với cột trụ, mặt phẳng Oxy là mặt nước và xem như trục Oy cùng phương với cầu như Hình 5.25. Dây cáp AD (xem như là một đoạn thẳng) đi qua đỉnh D thuộc trục Oz và điểm A thuộc mặt phẳng Oyz, trong đó điểm D là đỉnh cột trụ cách mặt nước 227 m, điểm A cách mặt nước 75 m và cách trục Oz 343 m. Giả sử ta dựng một đoạn dây nối N trên dây cáp AD và điểm M trên thành cầu, biết M cách mặt nước 75 m và MN song song với cột trụ.
a) Tính độ dài MN, biết điểm M cách trục Oz một khoảng bằng 230 m.
b) Người ta có thể dời đoạn dây dài 100 m để nối dây cáp AD với thành cầu tại vị trí điểm M cách trục Oz một khoảng bằng 148 m không? Vì sao?

- Xác định tọa độ các điểm A, D, M, và N dựa trên thông tin đề bài.
- Sử dụng phương trình tham số của đường thẳng AD để tính tọa độ điểm N với điều kiện đoạn MN song song với trục Oz.
- Tính độ dài đoạn MN bằng công thức khoảng cách giữa hai điểm trong không gian.
- Giải phương trình tham số cho đường thẳng AD với điều kiện mới (điểm M cách trục Oz một khoảng 148 m) để kiểm tra xem có thỏa mãn yêu cầu không.
a)
- Điểm A thuộc mặt phẳng Oyz, có tọa độ: \(A(0; - 343;75)\).
- Điểm D trên trục Oz, có tọa độ: \(D(0;0;227)\).
- Điểm M trên thành cầu, có tọa độ: \(M(0; - 230;75)\).
Vectơ chỉ phương của đường thẳng AD là:
\(\overrightarrow {AD} = D - A = (0 - 0;0 + 343;227 - 75) = (0;343;152)\)
Phương trình tham số của đường thẳng AD:
\(\left\{ {\begin{array}{*{20}{l}}{x = 0}\\{y = - 343 + 343t}\\{z = 75 + 152t}\end{array}} \right.\)
Trong đó, t là tham số.
Vì đoạn MN song song với trục Oz, nên tọa độ N sẽ có dạng \(N(0; - 230;{z_N})\). Để tìm \({z_N}\), ta thay \({y_N} = - 230\) vào phương trình tham số của AD:
\( - 230 = - 343 + 343t \Rightarrow t = \frac{{113}}{{343}}\)
Thay t vào phương trình tham số của z:
\({z_N} = 75 + 152 \times \frac{{113}}{{343}} \approx 125,1{\mkern 1mu} ({\rm{m}})\)
Vậy tọa độ của N là \(N(0; - 230;125,1)\).
Độ dài đoạn MN là:
\(MN = |{z_N} - {z_M}| = |125,1 - 75| = 50,1{\mkern 1mu} ({\rm{m}})\)
b)
Người ta muốn di chuyển dây cáp sao cho điểm M' cách trục Oz 148 m.
Xét điểm N' thuộc đường thẳng AD sao cho tọa độ \({y_{N'}} = - 148\).
Sử dụng phương trình tham số của đường thẳng AD, ta giải phương trình:
\( - 148 = - 343 + 343t \Rightarrow t = \frac{{195}}{{343}}\)
Thay giá trị của t vào phương trình của z, ta được:
\({z_{N'}} = 75 + 152 \times \frac{{195}}{{343}} \approx 161.4{\mkern 1mu} ({\rm{m}})\)
Sau khi di chuyển đoạn dây MN có độ dài:
\(MN = |161.4 - 75| = 86.4{\mkern 1mu} ({\rm{m}})\)
Vì độ dài đoạn dây nhỏ hơn 100 m, nên ta có thể nối dây cáp AD với thành cầu tại vị trí điểm M cách trục Oz một khoảng bằng 148m.

Các bài tập cùng chuyên đề
Tại một nút giao thông có hai con đường. Trên thiết kế, trong không gian Oxyz, hai con đường đó thuộc hai đường thẳng lần lượt có phương trình: \({\Delta _1}:\frac{{x - 1}}{2} = \frac{y}{{ - 1}} = \frac{{z + 1}}{3}\) và \({\Delta _2}:\frac{{x - 3}}{{ - 1}} = \frac{{y + 1}}{1} = \frac{z}{1}\).
a) Hai con đường trên có vuông góc với nhau hay không?
b) Nút giao thông trên có phải là nút giao thông khác mức hay không?
Trên mặt đất phẳng, người ta dựng một cây cột thẳng cao 6m vuông góc với mặt đất, có chân cột đặt tại vị trí O trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột 3m về hướng S60oE (hướng tạo với hướng nam góc \({60^o}\) và tạo với hướng đông góc \({30^o}\)) (H.5.32). Chọn hệ trục Oxyz có gốc tọa độ là O, tia Ox chỉ hướng nam, tia Oy chỉ hướng đông, tia Oz chứa cây cột, đơn vị đo là mét. Hãy viết phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét.
Một mô hình cầu treo được thiết kế trong không gian \(Oxyz\) như hình dưới đây. Viết phương trình tham số của làn đường \(d\) đi qua hai điểm \(M\left( {4;3;20} \right)\) và \(N\left( {4;1000;20} \right).\)

Trên một máy khoan bàn đã thiết lập sẵn một hệ toạ độ. Nêu nhận xét về vị trí giữa trục \(d\) của mũi khoan và trục \(d'\) của giá đỡ có phương trình lần lượt là \(d:\left\{ \begin{array}{l}x = 1\\y = 1\\z = 1 + t\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 10\\y = 20\\z = 5 + 5t'\end{array} \right.\)

Trên một phần mềm đã thiết kế sân khấu 3D trong không gian \(Oxyz\). Tính góc giữa hai tia sáng có phương trình lần lượt là: \(d:\frac{x}{2} = \frac{y}{1} = \frac{z}{{ - 1}}\) và \(d':\frac{{x - 1}}{3} = \frac{{y - 1}}{3} = \frac{{z - 1}}{9}\) (hình dưới đây).

Đề bài:
Trên một sân khấu đã thiết lập sẵn một hệ toạ độ \(Oxyz\). Tính góc giữa tia sáng có phương trình \(d:\left\{ \begin{array}{l}x = 2\\y = 1 + t\\z = 1 + t\end{array} \right.\) và măt sàn sân khấu có phương trình \(z = 0.\)

Để làm thí nghiệm về chuyển động trong mặt phẳng nghiêng, người làm thí nghiệm đã thiết lập sẵn một hệ toạ độ \(Oxyz\). Tính góc giữa mặt phẳng nghiêng \(\left( P \right):4x + 11z + 5 = 0\) và mặt sàn \(\left( Q \right):z - 1 = 0.\)
Trong trò chơi mô phỏng bắn súng 3D trong không gian \(Oxyz\), một xạ thủ đang ngắm với toạ độ khe ngắm và đầu ruồi lần lượt là \(M\left( {3;3;1,5} \right)\), \(N\left( {3;4;1,5} \right)\). Viết phương trình tham số của đường ngắm bắn của xạ thủ (xem như đường thẳng \(MN\)).

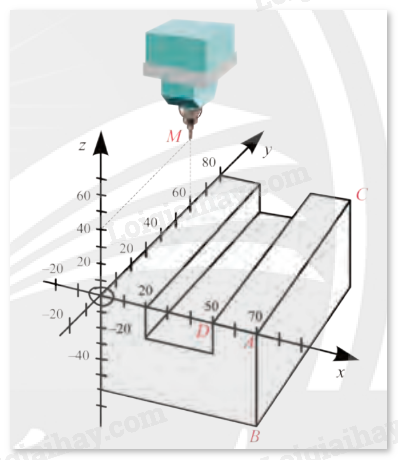
Phần mềm của máy tiện kĩ thuật số CNC (Computer Numerical Control) đang biểu diễn một chi tiết máy như hình dưới đây.
a) Tìm toạ độ các điểm \(A\), \(B\), \(C\), \(D\).
b) Viết phương trình mặt phẳng \(\left( {ABC} \right)\) và mặt phẳng \(\left( {ACD} \right)\).
c) Viết phương trình tham số của đường thẳng \(AC\).
d) Cho biết đầu mũi tiện đang đặt tại điểm \(M\left( {0;60;40} \right)\). Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {ABC} \right)\).
Trong không gian Oxyz, đường băng của một sân bay thuộc trục Oy. Một máy bay sau khi chạy đà trên đường băng đó đã cất cánh tại điểm \(A\left( {0;2;0} \right)\) với vận tốc không đổi trong khoảng thời gian ngắn ban đầu, vectơ vận tốc \(\overrightarrow v = \left( {1;4;1} \right)\). Hỏi trong khoảng thời gian ngắn nói trên, máy bay chuyển động trên đường thẳng nào và góc cất cánh của máy bay bằng bao nhiêu?
Trong không gian Oxyz, hai con đường tại một nút giao thông tương ứng thuộc hai đường thẳng:
\({\Delta _1}:\frac{{x - 1}}{1} = \frac{{y + 1}}{2} = \frac{z}{1}\) và \({\Delta _2}:\frac{{x + 1}}{3} = \frac{{y - 2}}{1} = \frac{{z + 1}}{4}\).
a) Nút giao thông trên có phải là nút giao thông khác mức hay không?
b) Tại nút giao thông nói trên, hai con đường tạo với nhau một góc bằng bao nhiêu độ?
Người ta muốn dựng một cột ăng-ten trên một sườn đồi. Ăng-ten được dựng thẳng đứng trong không gian \(Oxyz\) với độ dài đơn vị trên mỗi trục bằng 1 m. Gọi \(O\) là gốc cột, \(A\) là điểm buộc dây cáp vào cột ăng-ten và \(M,N\) là hai điểm neo dây cáp xuống mặt sườn đồi (Hình 6). Cho biết toạ độ các điểm nói trên lần lượt là \(O\left( {0;0;0} \right),A\left( {0;0;6} \right),M\left( {3; - 4;3} \right),\)\(N\left( { - 5; - 2;2} \right)\).
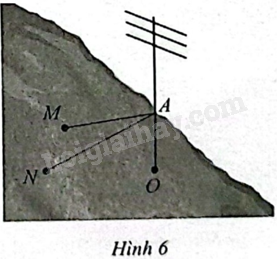
a) Tính độ dài các đoạn dây cáp \(MA\) và \(NA\).
b) Tính góc tạo bởi các sợi dây cáp \(MA,NA\) với mặt phẳng sườn đồi.
Anh Bình là một nhiếp ảnh gia chuyên săn ảnh chim hoang dã. Giả sử với hệ trục Oxyz cho trước, anh Bình đang ngắm và ống kính ở vị trí A có tọa độ \((200;685;436)\) thì có một con gà lôi tía xuất hiện ở vị trí B có tọa độ \((640;550;474)\).
a) Viết phương trình tham số của đường thẳng chứa đoạn thẳng nối hai vị trí ống kính ngắm của anh Bình và con gà lôi tía.
b) Nếu một quả đồi có tọa độ đỉnh C là \((420;617,5;450)\). Hỏi C có thuộc đường ngắm AB không? Anh Bình có ngắm thấy con gà lôi tía này không?
Trong một khu du lịch, người ta cho du khách trải nghiệm thiên nhiên bằng cách đu theo đường trượt zipline từ vị trí A cao 15 m của tháp 1 này sang vị trí B cao 10 m của tháp 2 trong khung cảnh tuyệt đẹp xung quanh. Với hệ trục tọa độ Oxyz cho trước (đơn vị: mét), tọa độ của A và B lần lượt là \(A(3;2,5;15)\) và \(B(21;27,5;10)\).

a) Viết phương trình đường thẳng chứa đường trượt zipline này.
b) Xác định tọa độ của du khách khi ở độ cao 12 mét.
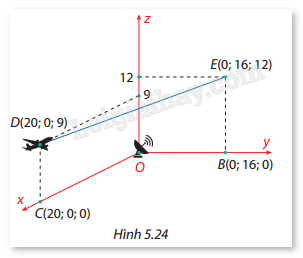
Giả sử một máy bay thương mại M đang bay trên bầu trời theo một đường thẳng từ D đến E có hình chiếu trên mặt đất là đoạn CB. Tại D, máy bay bay cách mặt đất là 9000 m và tại E là 12000 m. Một ra-đa được đặt trên mặt đất tại vị trí O cách C là 20000 m, cách B là 16000 m và \(\widehat {BOC} = {90^\circ }\). Xét hệ trục tọa độ Oxyz (đơn vị: 1000 m) với O là vị trí đặt ra-đa, B thuộc tia Oy, C thuộc tia Ox, khi đó ta có tọa độ các điểm như Hình 5.24. Giả sử ra-đa có bán kính dò tìm tối đa là 16000 m. Hỏi ra-đa này có thể dò tìm được tín hiệu của máy bay M khi bay trên bầu trời từ D đến E hay không? Vì sao?
Trong hệ trục tọa độ Oxyz, với mặt phẳng (Oxy) là mặt đất, một máy bay cất cánh từ vị trí \(A(0;10;0)\) với vận tốc \(\vec v = (150;150;40)\).
a) Viết công thức tính tọa độ của máy bay trong 2 giờ đầu tiên.
b) Tính góc nâng của máy bay (góc giữa hướng chuyển động bay lên của máy bay với đường bằng) và làm tròn kết quả đến hàng đơn vị.
Trong không gian với hệ tọa độ Oxyz, cần một xe container di chuyển trên mặt phẳng (Oxy) và chui qua gầm của một cây cầu. Cây cầu đó thuộc đường thẳng d: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 1 + t\\z = 3\end{array} \right.\). Hỏi xe container có chiều cao nào dưới đây có thể chui được qua gầm cầu?
-
A.
2,8
-
B.
3,1
-
C.
3,2
-
D.
4,2
Trong các chương trình đồ hoạ máy tính, để tạo ảo giác theo đúng phối cảnh, các vật ở càng gần thì càng lớn hơn các vật ở xa, các hình ảnh ba chiều trong bộ nhớ của máy tính được chiếu lên một màn hình hình chữ nhật từ điểm nhìn của mắt hoặc máy chiếu.
Không gian quan sát, một phần của không gian được nhìn thấy là vùng nằm trong bốn mặt phẳng đi qua điểm nhìn và một đường biên của màn hình. Nếu vật trong cảnh vật mở rộng vượt quá bốn mặt phẳng này thì chúng phải được cắt xén trước khi dữ liệu điểm ảnh được gửi đến màn hình. Vì vậy các mặt phẳng này được gọi là mặt phẳng cắt. Giả sử màn hình được biểu diễn bởi hình chữ nhật trong mặt phẳng Oyz với các đỉnh (0; 400; 0), (0; −400; 0), (0; 400; 600), (0; −400; 600) và máy quay được đặt tại (1000; 0; 0). Tính góc giữa màn hình và các mặt phẳng cắt.
Một tháp phát sóng cao 50 m đặt ở góc A của sân hình chữ nhật ABCD. Để giữ cho tháp không bị đổ, người ta có cột rất nhiều dây cáp quanh tháp và cố định tại các vị trí trên mặt đất. Hai chú kiến vàng và kiến đen bắt đầu leo lên hai dây cáp CM và BN (từ C và B) với vận tốc lần lượt là 3 m/phút và 2,5 m/phút. Hỏi sau 10 phút thì hai chú kiến cách nhau bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?

Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục toạ độ là kilomet), một máy bay đang ở vị trí A(3,5;2;0,4) và sẽ hạ cánh ở vị trí B(3,5;5,5;0) trên đường băng EG (hình vẽ).
a) Đường thẳng AB có phương trình tham số là \(\left\{ \begin{array}{l}x = 3,5\\y = - 2 + 7,5t\\z = 0,4 - 0,4t\end{array} \right.\) \((t \in \mathbb{R})\).
b) Khi máy bay ở vị trí D(3,5;3,25;0,12) thì máy bay cách mặt đất 120 m.
c) Có một lớp mây được mô phỏng bởi một mặt phẳng \((\alpha )\) đi qua ba điểm M(5;0;0), N(0;-5;0), P(0;0;0,5). Vị trí mà máy bay xuyên qua đám mây để hạ cánh là \(C\left( {\frac{7}{2};\frac{{47}}{{44}};\frac{{13}}{{55}}} \right)\).
d) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu E(3,5;4,5;0) của đường băng ở độ cao tối thiểu là 120 m. Nếu sau khi ra khỏi đám mây, tầm nhìn của người phi công là 900 m thì người phi công đã không đạt được quy định an toàn bay.
(Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
Một máy bay đang di chuyển về phía sân bay. Tại thời điểm hiện tại, vị trí của máy bay là B(150;150;5000) (trong đó 5000m là độ cao của máy bay so với mặt đất). Máy bay đang di chuyển thẳng tới sân bay với vận tốc 700 km/h. Sân bay có tọa độ C(0;0;0) và máy bay đang tiến dần đến vị trí hạ cánh tại sân bay.
a) Phương trình tham số của đường thẳng mà máy bay di chuyển theo là \(\left\{ \begin{array}{l}x = 150 - 150t\\y = 150 - 150t\\z = 5000 - 5000t\end{array} \right.\).
b) Khoảng cách từ vị trí hiện tại của máy bay B(150;150;5000) đến sân bay C(0;0;0) là \(\sqrt {15250000} \approx 3905,6\) km.
c) Với vận tốc của máy bay là 700km/h, thời gian để máy bay hạ cánh là khoảng 5,5 giờ.
d) Hệ thống kiểm soát không lưu yêu cầu liên lạc với máy bay khi nó còn cách sân bay 40km. Khi máy bay ở vị trí (6;6;200), nó còn cách sân bay 40 km.
Các thiên thạch có đường kính lớn hơn 140 m và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn 7500000 km được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, người ta đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất. Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá 6630 km so với mực nước biển. Coi Trái Đất là khối cầu có bán kính 6370 km. Chọn hệ trục tọa độ Oxyz trong không gian có gốc O tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là 1000 km. Một thiên thạch (coi như một hạt) chuyển động với tốc độ không đổi theo một đường thẳng từ điểm M(-12;29;10) theo phương song song với giá của vecto \(\overrightarrow u ( - 12;17;5)\).
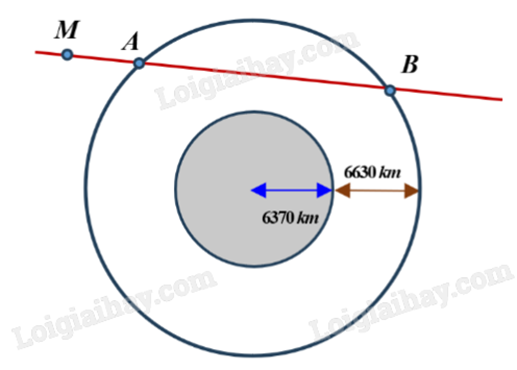
a) Trong hệ trục tọa độ đã cho thiên thạch di chuyển trên đường thẳng có phương tham số \(\left\{ \begin{array}{l}x = - 12 - 12t\\y = 29 + 17t\\z = 10 + 5t\end{array} \right.\), \(t \in \mathbb{R}\).
b) Vị trí đầu tiên thiên thạch di chuyển vào phạm vi theo dõi của hệ thống quan sát là điểm A(12;-5;0).
c) Vị trí cuối cùng mà thiên thạch di chuyển trong phạm vi theo dõi của hệ thống quan sát là B(0;12;5).
d) Thiên thạch trên không va vào trái đất.
Trong không gian Oxyz, đài kiểm soát không lưu sân bay có tọa độ O(0;0;0), đơn vị trên mỗi trục tính theo kilômét. Một máy bay chuyển động hướng về đài kiểm soát không lưu, bay qua hai vị trí A(-500;-250;150), B(-200;-200;100). Khi máy bay ở gần đài kiểm soát nhất, tọa độ của vị trí máy bay là (a;b;c). Giá trị của biểu thức -3a - b - c là bao nhiêu (làm tròn kết quả đến hàng đơn vị)?
Trong một khu du lịch, người ta cho du khách trải nghiệm thiên nhiên bằng cách đu theo đường trượt zipline từ vị trí A cao 15 m của tháp 1 này sang vị trí B cao 10 m của tháp 2 trong khung cảnh tuyệt đẹp xung quanh. Với hệ trục toạ độ Oxyz cho trước (đơn vị: mét), toạ độ của A và B lần lượt là (3; 2,5; 15) và (21; 27,5; 10). Xác định toạ độ của du khách khi ở độ cao 12 mét.

Trong không gian, một cabin cáp treo xuất phát từ điểm A(-3;1;6) và chuyển động theo đường cáp có vecto chỉ phương là \(\overrightarrow u = (1; - 2;6)\) với tốc độ là 6 m/s (đơn vị trên mỗi trục tọa độ là mét). Giả sử sau 8 (s) kể từ lúc xuất phát, cabin đến điểm B. Gọi tọa độ B(a;b;c). Tính a + b + c, kết quả làm tròn đến hàng phần mười.
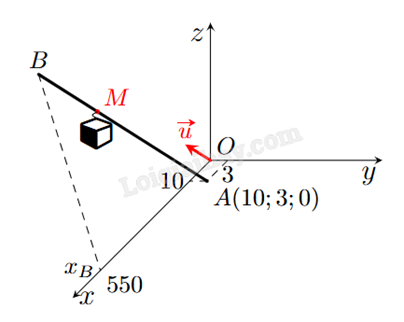
Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10;3;0) và chuyển động đều theo đường cap có vecto chỉ phương là \(\overrightarrow u = (2; - 2;1)\) với tốc độ là 4,5 m/s (đơn vị trên mỗi trục tọa độ là mét). Sau thời gian 180 giây, cabin dừng ở điểm B. Tìm tung độ điểm B.
Trong không gian với hệ tọa độ Oxyz, một chiếc máy bay cất cánh từ điểm P(15;-4;2) và bay đều theo hướng của vecto \(\overrightarrow d = (3;1; - 2)\) với tốc độ 5 m/s. Sau thời gian 200 giây, máy bay đến điểm Q. Tìm tung độ điểm Q (kết quả làm tròn đến hàng đơn vị).
Tại một nút giao thông có hai con đường. Trên thiết kế, trong không gian Oxyz, hai con đường đó thuộc hai đường thẳng lần lượt có phương trình là \({d_1}\): \(\left\{ \begin{array}{l}x = 1 + at\\y = t\\z = - 1 + 2t\end{array} \right.\) và \({d_2}\): \(\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z - 3}}{1}\). Tìm a để nút giao thông trên là nút giao thông cùng mức.
Trong không gian, có một chiếc máy bay không người lái tại điểm M(3;-1;4). Cho biết quỹ đạo bay của máy bay này là đường thẳng \(\Delta \) có vecto chỉ phương (-1;b;c) và biết rằng quỹ đạo phải song song với mặt đất (mặt phẳng (Oxy)) đồng thời vuông góc với hướng của một chiếc máy bay khác theo đường thẳng d: \(\frac{{x + 1}}{2} = \frac{y}{{ - 1}} = \frac{{z - 3}}{3}\). Tính b + c.
Trong không gian Oxyz, một cabin cáp treo ở Bà Nà Hill xuất phát từ điểm A(-2;1;5) và chuyển động đều theo đường cáp có vecto chỉ phương là \(\overrightarrow u = (0; - 2;6)\) với tốc độ là 4 m/s (đơn vị trên mỗi trục tọa độ là mét). Giả sử sau 5 giây (s) kể từ lúc xuất phát, cabin đến điểm M. Gọi tọa độ M(a;b;c). Tính a + 3b + c.







