Bảng 3.13 là mẫu số liệu ghép nhóm về lương của 40 nhân viên công ty M mà anh Bình có:
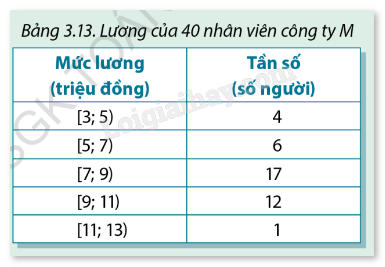
a) Hãy ước tính lương trung bình \({\overline X _M}\) của 40 nhân viên.
b) Điều anh Bình quan tâm là độ lệch trung bình giữa lương của mỗi nhân viên so với lương trung bình \({\overline X _M}\). Anh Bình có thể ước lượng độ lệch giữa lương của những nhân viên thuộc nhóm thứ nhất (nhóm lương từ 3 đến dưới 5 triệu đồng) so với số trung bình qua giá trị nào?
c) Dựa vào công thức tính trung bình của mẫu số liệu ghép nhóm và hai công thức tính phương sai, độ lệch chuẩn của mẫu số liệu không ghép nhóm, hãy đề xuất một cách ước tính phương sai và độ lệch chuẩn của mẫu số liệu gốc mà anh Bình không có (bảng lương của từng người).
a) Công thức tính điểm trung bình
\({\bar X_M} = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\), trong đó:
- \({x_i}\) là giá trị đại diện của khoảng lương thứ \(i\).
- \({n_i}\) là tần số của khoảng lương thứ \(i\).
- \(N\) là tổng số nhân viên.
b) Sử dụng giá trị trung bình của nhóm lương từ 3 đến dưới 5 triệu đồng.
Công thức:
\(\Delta = \left| {{x_{[3;5)}} - {{\overline X }_M}} \right|\)
c)
- Công thức tính phương sai của mẫu số liệu không ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
a) Tính lương trung bình \({\overline X _M}\):
\(\begin{array}{l}[3;5):\frac{{3 + 5}}{2} = 4;\\(5;7):\frac{{5 + 7}}{2} = 6{\rm{ }};\\(7;9):\frac{{7 + 9}}{2} = 8{\rm{ }};\\(9;11)\frac{{9 + 11}}{2} = 10{\rm{ }};\\(11;13)\frac{{11 + 13}}{2} = 12{\rm{ }}\end{array}\)
Lương trung bình:
\({\overline X _M} = \frac{{\sum {{x_i}.{n_i}} }}{N} = \frac{{4.4 + 6.6 + 8.17 + 10.12 + 12.1}}{{40}} = 8\)
b) Ước lượng độ lệch trung bình:
Giá trị đại diện của nhóm thứ nhất (3 đến 5 triệu đồng): 4 triệu đồng
Độ lệch giữa lương của nhóm này và lương trung bình là:
\(\Delta = \left| {{x_{[3;5)}} - {{\overline X }_M}} \right| = \left| {4 - 8} \right| = 4\) triệu đồng
c)
Công thức tính trung bình là
\({\bar X_M} = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\)
Công thức tính phương sai của mẫu số liệu không ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2}\)
Ta biết rằng các giá trị \({x_i}\) nằm trong các nhóm, và mỗi nhóm có trung điểm \({x_j}\) và tần số \({n_j}\). Do đó, ta có thể viết lại tổng trên bằng cách thay thế từng \({x_i}\) trong mỗi nhóm bằng trung điểm \({x_j}\):
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2} = \frac{1}{N}\sum\limits_{j = 1}^k {\sum\limits_{i = 1}^{{n_j}} {{{({x_i} - \overline x )}^2}} } = \frac{1}{N}\sum\limits_{j = 1}^k {{n_j}({x_j}} - \overline x {)^2}\)
Vậy công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{j = 1}^k {{n_j}({x_j}} - \overline x {)^2}\)
Và độ lệch chuẩn của mẫu số liệu ghép nhóm vẫn là:
\(S = \sqrt {{S^2}} \).

Các bài tập cùng chuyên đề
Trở lại bài toán trong tình huống mở đầu, gọi \({x_1},{x_2},...,{x_{20}}\) là các kết quả đo (mẫu số liệu gốc).
a) Có thể tính được chính xác phương sai và độ lệch chuẩn của mẫu số liệu gốc hay không?
b) Thảo luận và đề xuất ước lượng cho phương sai và độ lệch chuẩn của mẫu số liệu gốc.
Xét mẫu số liệu ghép nhóm cho bởi bảng 13
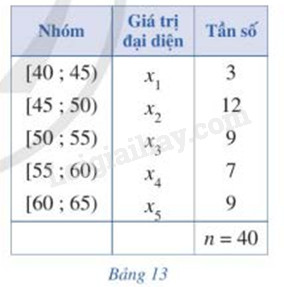
a) Tìm \({x_1},{x_2},{x_3},{x_4},{x_5}\) lần lượt là giá trị đại diện của nhóm 1, nhóm 2, nhóm 3, nhóm 4, nhóm 5
b) Tính số trung bình cộng \(\overline x \) của mẫu số liệu ghép nhóm đó
c) Tính \({s^2} = \frac{{3.{{({x_1} - \overline x )}^2} + 12{{({x_2} - \overline x )}^2} + 9{{({x_3} - \overline x )}^2} + 7{{({x_4} - \overline x )}^2} + 9{{({x_5} - \overline x )}^2}}}{{40}}\)
d) Tính \(s = \sqrt {{s^2}} \)
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong bảng 18.
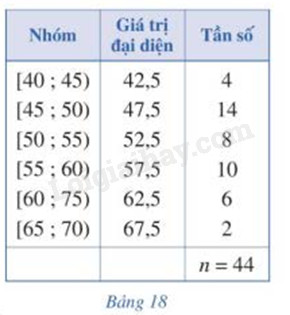
a) Phương sai của mẫu số liệu ghép nhóm trên là:
A. 53,2
B. 46,1
C. 30
D. 11
b) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
A. 6,8
B. 7,3
C. 3,3
D. 46,1
Bảng 21 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố. Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
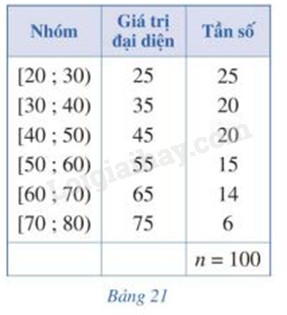
Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm ở Khởi động

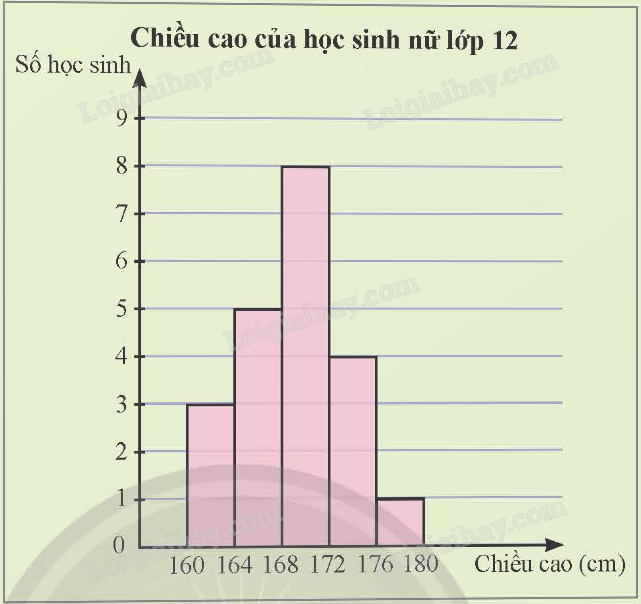
a) Trong biểu đồ ở Khởi động, cột thứ nhất biểu diễn số lượng học sinh có chiều cao từ 160cm đến dưới 164cm; cột thứ hai biểu diễn số lượng học sinh có chiều cao từ 164cm đến dưới 168cm, … .

Hãy lập bảng tần số ghép nhóm cho mẫu số liệu ở , xác định giá trị đại diện của mỗi nhóm và tính số trung bình của mẫu số liệu ghép nhóm.
b) Xét mẫu số liệu mới gồm các giá trị đại diện của các nhóm, tần số của mỗi giá trị đại diện bằng tần số của nhóm tương ứng. Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu mới.
Bảng dưới đây thống kê cự li ném tạ của một vận động viên.

Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Chọn khẳng định sai trong các khẳng định sau:
-
A.
Phương sai luôn là một số không âm.
-
B.
Phương sai là bình phương của độ lệch chuẩn.
-
C.
Phương sai càng lớn thì độ phân tán so với số trung bình cộng càng lớn.
-
D.
Phương sai luôn lớn hơn độ lệch chuẩn.
Khẳng định nào sau đây đúng?
-
A.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là căn bậc ba số học của phương sai của mẫu số liệu ghép nhóm.
-
B.
Phương sai của mẫu số liệu ghép nhóm là căn bậc ba số học của độ lệch chuẩn của mẫu số liệu ghép nhóm.
-
C.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm.
-
D.
Phương sai của mẫu số liệu ghép nhóm là căn hai số học của độ lệch chuẩn của mẫu số liệu ghép nhóm.
Một mẫu số liệu ghép nhóm có phương sai bằng 4 thì có độ lệch chuẩn bằng bao nhiêu?
-
A.
4
-
B.
-4
-
C.
2
-
D.
8
Cho mẫu số liệu ghép nhóm về tuổi thọ của 20 thiết bị điện tử sau:

Phương sai của mẫu số liệu ghép nhóm trên là
A. 1,99.
B. 2,99.
C. 3,99.
D. 4,99.
Cho mẫu số liệu ghép nhóm về tuổi thọ của 20 thiết bị điện tử sau:
Nếu thay các nhóm tương ứng bằng \(\left[ {3;5} \right),{\rm{ }}\left[ {5;7} \right),{\rm{ }}\left[ {7;9} \right),{\rm{ }}\left[ {9;11} \right)\) thì độ lệch chuẩn sẽ thay đổi như thế nào?
A. Tăng.
B. Giảm.
C. Không thay đổi.
Cho mẫu số liệu ghép nhóm về tuổi thọ của 20 thiết bị điện tử sau:

Nếu thay các tần số tương ứng bằng 1, 9, 9, 1 thì độ lệch chuẩn sẽ thay đổi như thế nào?
A. Tăng.
B. Giảm.
C. Không thay đổi.
Một mẫu số liệu ghép nhóm có độ lệch chuẩn bằng 9 thì có phương sai bằng bao nhiêu?
A. 9.
B. 3.
C. 18.
D. 81.
Một mẫu số liệu ghép nhóm có phương sai bằng 16 thì có độ lệch chuẩn bằng bao nhiêu?
A. 4.
B. 8.
C. 256.
D. 32.
Bảng 18 thống kê mật độ dân số (đơn vị: người/km2) của 23 tỉnh, thành phố thuộc vùng Trung du và miền núi phía Bắc, Đồng bằng sông Hồng (không kể thành phố Hà Nội và tỉnh Bắc Ninh) trong năm 2021 (Nguồn: Niên giám Thống kê 2021, NXB Thống kê, 2022).
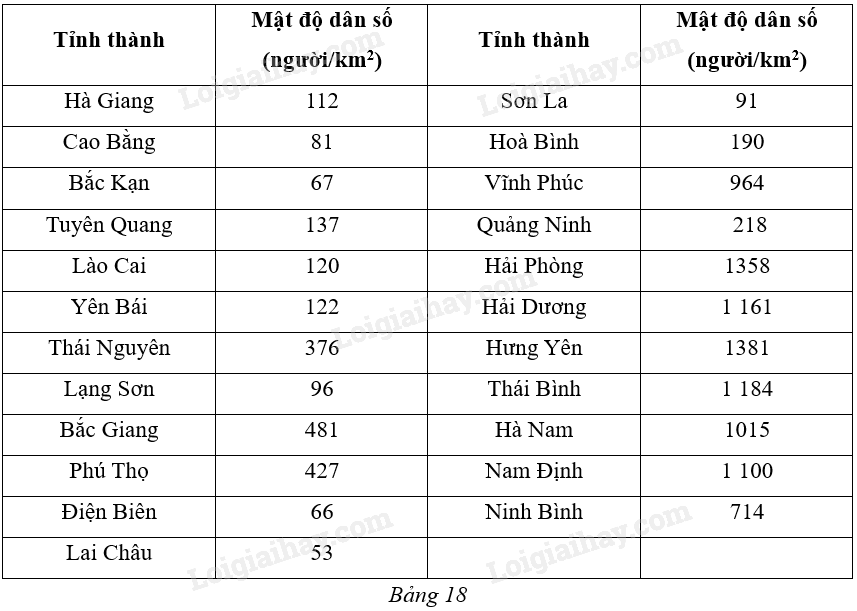
a) Lập bảng tần số ghép nhóm của mẫu số liệu cho bởi Bảng 18 theo bảy nhóm:
\(\left[ {0;200} \right);\left[ {200;400} \right);\left[ {400;600} \right);\left[ {600;800} \right);\left[ {800;1000} \right);\left[ {1000;1200} \right);\left[ {1200;1400} \right)\).
b) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng đơn vị).
Thời gian bù giờ của 64 trận đấu bóng đá trong một giải đấu được ghi lại ở bảng sau:

Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Thầy giáo cho các bạn học sinh lớp 8 vận dụng khái niệm tam giác đồng dạng để thực hành đo chiều cao của cột cờ. Kết quả đo của các bạn trong lớp được biểu diễn ở bảng sau:

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Chiều cao của một số cây giống sau khi nảy mầm được 4 tuần được biểu diễn ở bảng sau:
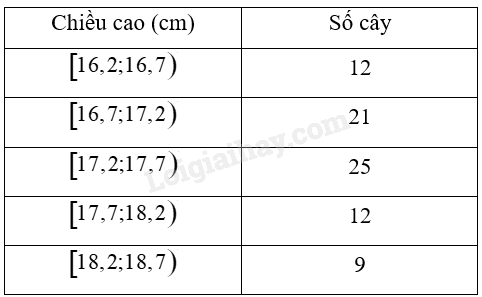
Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Bác Xuân biểu diễn thời gian tập thể dục mỗi ngày của mình trong 120 ngày liên tiếp ở biểu đồ tần số tương đối nghép nhóm dưới đây.
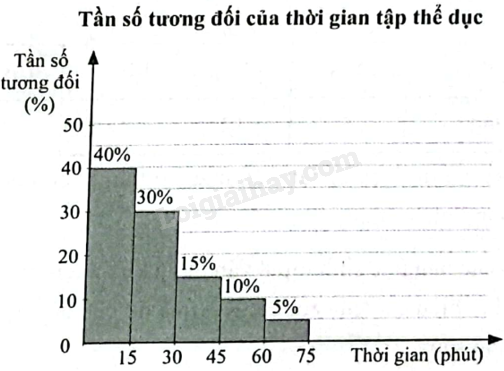
a) Lập bảng tần số ghép nhóm cho dữ liệu ở biểu đồ trên.
b) Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Số tiền ghi trên hoá đơn của 150 khách hàng lấy ngẫu nhiên trong một ngày được siêu thị ghi lại ở bảng dưới đây:

Tìm phương sai, độ lệch chuẩn của mẫu số liệu về số tiền ghi trên hoá đơn.
Điều tra chi phí thuê nhà ở hàng tháng của một số nhân viên độc thân, công ty X thu được số liệu dưới đây:

Tính trung bình và độ lệch chuẩn chi phí thuê nhà hàng tháng của những nhân viên được điều tra.
Phương sai của mẫu số liệu cho bởi bảng 3.30 là

A. \({s^2} = \frac{8}{{15}} - {\left( {\frac{7}{{15}}} \right)^2}\).
B. \({s^2} = \frac{{233}}{{15}} - {\left( {\frac{{50}}{{15}}} \right)^2}\).
C. \({s^2} = \frac{8}{{15}} - {\left( {\frac{{57}}{{15}}} \right)^2}\).
D. \({s^2} = \frac{{233}}{{15}} - {\left( {\frac{{57}}{{15}}} \right)^2}\).
Trong các khẳng định sau, khẳng định nào sai?
A. Phương sai luôn luôn là số không âm.
B. Phương sai là bình phương của độ lệch chuẩn.
C. Phương sai càng lớn thì độ phân tán của các giá trị quanh số trung bình càng lớn.
D. Phương sai luôn luôn lớn hơn độ lệch chuẩn.
Bảng tần số ghép nhóm sau cho biết thành tích luyện tập của một vận động viên nghiệp dư chạy maraton 42 km.

Độ lệch chuẩn của mẫu số liệu ghép nhóm (làm tròn đến chữ số hàng phần trăm) là
A. 0,51.
B. 0,61.
C. 0,71.
D. 0,81.
Để đánh giá mức độ ổn định của một loại pin điện, người ta thống kê thời gian sử dụng liên tục của pin khi được sạc đầy điện theo bảng mẫu số liệu sau:

Hãy cho biết độ lệch chuẩn của mẫu số liệu gần nhất với giới trị nào sau đây?
-
A.
0,518
-
B.
0,529
-
C.
0,720
-
D.
1,120
Hai mẫu số liệu ghép nhóm \({M_1},{M_2}\) có bảng tần số ghép nhóm như sau:
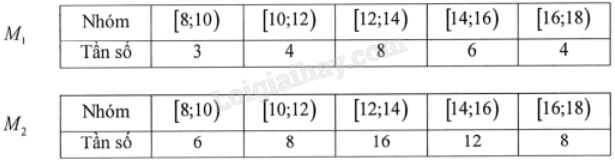
Gọi \({s_1},{s_2}\) lần lượt là độ lệch chuẩn của mẫu số liệu ghép nhóm \({M_1},{M_2}\). Phát biểu nào sau đây là đúng?
-
A.
\({s_1} = {s_2}\).
-
B.
\({s_1} = 2{s_2}\).
-
C.
\(2{s_1} = {s_2}\).
-
D.
\(4{s_1} = {s_2}\).
Khảo sát thời gian chơi thể thao trong một ngày của 42 học sinh được cho trong bảng sau (thời gian đơn vị phút):

Phương sai của mẫu số liệu (được làm tròn đến hàng đơn vị) bằng
-
A.
598
-
B.
597
-
C.
2477
-
D.
256
Một bệnh viện thống kê lại số cân nặng của 20 bé sơ sinh trong bảng sau:

Phương sai của mẫu số liệu ghép nhóm là
-
A.
3,39
-
B.
11,62
-
C.
0,1314
-
D.
0,36
Có thể tính phương sai và độ lệch chuẩn của số liệu ở biểu đồ trên hay không?