Cho hình chữ nhật ABCD và cho M là trung điểm của đoạn thẳng AB như hình vẽ dưới đây. Chứng minh rằng M nằm trên đường trung trực của CD.
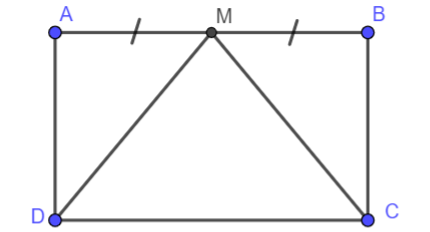
Chứng minh MD = MC.
Hai tam giác MAD và MBC lần lượt vuông tại A, B và có:
MA = MB (M là trung điểm AB)
DA = CB (hai cạnh đối của hình chữ nhật)
Vậy \(\Delta MAD = \Delta MBC\)(hai cạnh góc vuông). Do đó MD = MC. Vậy M cách đều hai đầu của đoạn thẳng CD.
Do đó M nằm trên đường trung trực của đoạn thẳng CD.
+ Định nghĩa đường trung trực: Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó.
Ví dụ: Nếu đường thẳng $d$ là đường trung trực của đoạn thẳng $AB$, thì $d$ phải đi qua trung điểm của $AB$ và $d \perp AB$.
+ Tính chất của đường trung trực (Định lý thuận): Bất kỳ điểm nào nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Điều này có nghĩa là, nếu điểm $P$ nằm trên đường trung trực của đoạn thẳng $XY$, thì $PX = PY$.
+ Dấu hiệu nhận biết đường trung trực (Định lý đảo): Tập hợp tất cả các điểm cách đều hai mút của một đoạn thẳng chính là đường trung trực của đoạn thẳng đó.
Điều này có nghĩa là, nếu bạn chứng minh được một điểm $P$ cách đều hai mút $X$ và $Y$ của một đoạn thẳng (tức là $PX = PY$), thì điểm $P$ đó nằm trên đường trung trực của đoạn thẳng $XY$.
Trong bài toán đã cho, chúng ta cần chứng minh rằng điểm M nằm trên đường trung trực của đoạn thẳng CD.
Dựa vào tính chất đảo của đường trung trực (dấu hiệu nhận biết), để chứng minh M nằm trên đường trung trực của CD, ta cần chứng minh rằng M cách đều hai mút của đoạn thẳng CD, tức là $MD = MC$.
Phương pháp giải chung cho dạng bài này
Để chứng minh một điểm $P$ nằm trên đường trung trực của một đoạn thẳng $XY$, phương pháp chung và hiệu quả nhất là chứng minh rằng điểm $P$ cách đều hai mút của đoạn thẳng đó ($PX = PY$).
Các bước thực hiện thường bao gồm:
+ Xác định mục tiêu: Để chứng minh $P$ nằm trên đường trung trực của $XY$, ta cần chứng minh $PX = PY$.
+ Tìm kiếm các tam giác liên quan: Thường là các tam giác có chứa $PX$ và $PY$ làm các cạnh tương ứng.
+ Thu thập thông tin: Liệt kê các yếu tố đã biết hoặc có thể suy ra từ giả thiết (ví dụ: các đoạn thẳng bằng nhau, các góc bằng nhau, các góc vuông, trung điểm, tính chất của các hình đặc biệt như hình chữ nhật, tam giác cân...).
+ Chứng minh hai tam giác bằng nhau: Sử dụng các trường hợp bằng nhau của tam giác (cạnh - cạnh - cạnh, cạnh - góc - cạnh, góc - cạnh - góc) hoặc các trường hợp đặc biệt cho tam giác vuông (cạnh huyền - góc nhọn, cạnh huyền - cạnh góc vuông, hai cạnh góc vuông) để chứng minh hai tam giác đã chọn ở bước 2 là bằng nhau.
+ Suy ra sự bằng nhau của các đoạn thẳng: Từ sự bằng nhau của hai tam giác, suy ra các cạnh tương ứng bằng nhau, tức là $PX = PY$.
+ Kết luận: Vì $P$ cách đều $X$ và $Y$, nên $P$ nằm trên đường trung trực của đoạn thẳng $XY$.
Lưu ý:
Một số bài toán có thể yêu cầu chứng minh ngược lại, tức là chứng minh một đường thẳng là đường trung trực của một đoạn thẳng. Khi đó, ta cần chứng minh đường thẳng đó đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.

Các bài tập cùng chuyên đề
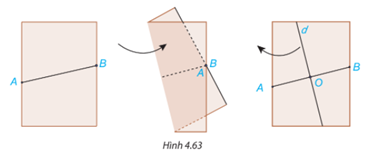
Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB.
Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau. Mở mảnh giấy ra, kẻ một đường thẳng d theo nếp gấp.
a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?
b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?
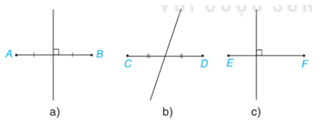
Trong Hình 4.64, bạn Lan vẽ đường trung trực của các đoạn thẳng. Theo em, hình nào Lan vẽ đúng?
Trên mảnh giấy trong HĐ3, lấy điểm M bất kì trên đường thẳng d. Dùng thước thẳng có vạch chia kiểm tra xem AM có bằng BM không (H.4.65).
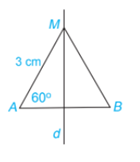
Cho M là một điểm nằm trên đường trung trực của đoạn thẳng AB. Biết AM = 3 cm và \(\widehat {MAB}\)= 60° (H.4.67). Tính BM và số đo góc MBA.
Trong Hình 4.70, đường thẳng nào là đường trung trực của đoạn thẳng AB?
Cho tam giác ABC cân tại A có đường cao AD. Chứng minh rằng đường thẳng AD là đường trung trực của đoạn thẳng BC.
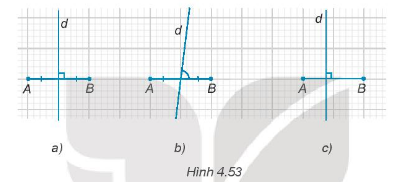
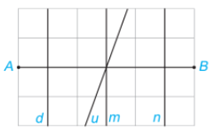
Đường thẳng d trong hình nào dưới đây là đường trung trực của đoạn thẳng AB?
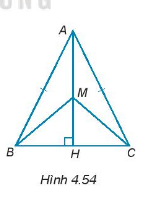
Cho A là một điểm tuỳ ý nằm trên đường trung trực của đoạn thẳng BC sao cho A không thuộc BC. Khẳng định nào dưới đây là đúng?
a) AB = AC
b) Tam giác ABC đều
c) \(\widehat {ABC} = \widehat {ACB}\)
d) Tam giác ABC cân tại đỉnh A.
Trong các câu sau đây, câu nào đúng?
A. Đường thẳng đi qua trung điểm của đoạn thẳng AB là đường trung trực của đoạn thẳng AB.
B. Đường thẳng vuông góc với đoạn thẳng AB là đường trung trực của đoạn thẳng AB.
C. Tập hợp các điểm cách đều hai điểm phân biệt A và B là đường thẳng đi qua trung điểm của đoạn thẳng AB.
D. Đường thẳng đi qua trung điểm và vuông góc với đoạn thẳng AB là đường trung trực của đoạn thẳng AB.
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59)
a) Chứng minh rằng MP = MQ và AP = AQ
b) Đường thẳng PQ có vuông góc với AM không? Vì sao?

Đường thẳng d là đường trung trực của đoạn thẳng AB khi và chỉ khi
A. d đi qua trung điểm AB.
B. d là trục đối xứng của AB.
C. d vuông góc với AB.
D. d vuông góc với AB tại trung điểm của AB.
Trong hình dưới đây, đường thẳng nào là đường trung trực của đoạn thẳng AB.
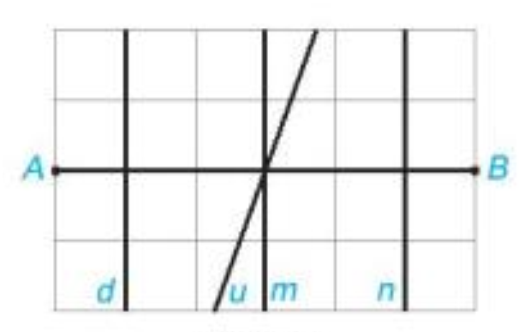
Cho tam giác ABC cân tại A có đường cao AD. Chứng minh rằng đường thẳng AD là đường trung trực của đoạn thẳng BC.

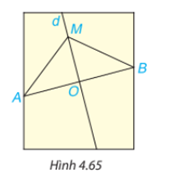
Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm AB, AC. Gọi O là giao diểm của đường thẳng BN và CM. Chứng minh rằng O nằm trên đường trung trực của đoạn thẳng BC.
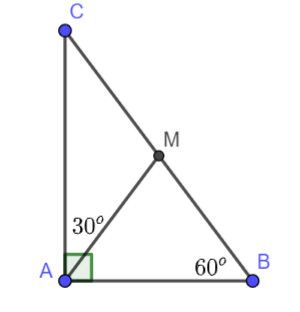
Cho tam giác ABC vuông tại A có \(\widehat B = {60^o}\). Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng
a) Tam giác CAM cân tại M
b) Tam giác BAM đều
c) M là trung điểm của đoạn thẳng BC.
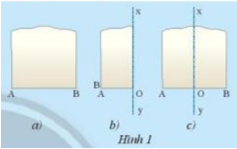
Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b)
Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao?
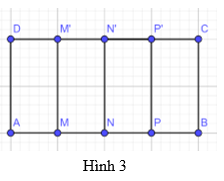
Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N, P và trên cạnh DC lấy các điểm M’, N’, P’. Cho biết AM = MN = NP = PB và MM’, NN’, PP’ đều song song với BC (Hình 3). Tìm đường trung trực của mỗi đoạn thẳng AB, AN và NB.
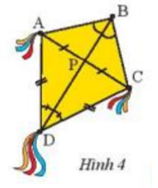
Trong Hình 4, hãy cho biết BD có là đường trung trực của đoạn thẳng AC hay không? Tại sao?
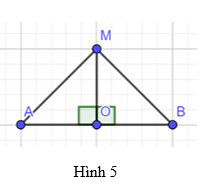
Cho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5). Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB
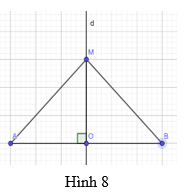
Trong Hình 8, cho biết d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = x + 2 và MB = 7. Tính x
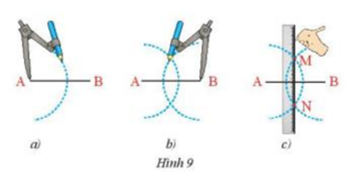
Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau:
- Lấy A làm tâm vẽ cung tròn bán kính lớn hơn \(\dfrac{1}{2}\)AB (Hình 9a)
- Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b)
- Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN. Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB.
Hình 10 minh họa một tờ giấy có hình vẽ đường trung trực xy của đoạn thẳng AB mà hình ảnh điểm B bị nhòe mất. Hãy nêu cách xác định điểm B.
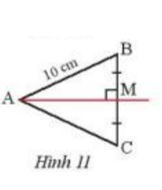
Quan sát Hình 11, cho biết M là trung điểm của BC, AM vuông góc với BC và AB = 10 cm, Tính AC.
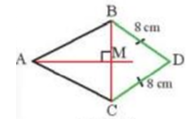
Quan sát Hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm. Chứng minh rằng ba điểm A, M, D thẳng hàng.
Quan sát Hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC.

Cho hai điểm M và N nằm trên đường trung trực d của đoạn thẳng EF. Chứng minh rẳng \(\Delta EMN=\Delta FMN\)
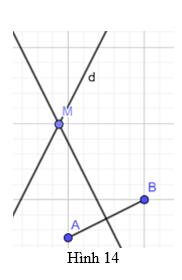
Trên bản đồ qui hoạch một khu dân cư có một con đường d và hai điểm dân cư A và B (Hình 14). Hãy tìm bên đường một địa điểm M để xây dựng một trạm y tế sao cho trạm y tế cách đều hai điểm dân cư.
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
-
A.
Trung trực;
-
B.
Giao điểm;
-
C.
Trọng tâm;
-
D.
Trung điểm.
Hình 86 minh họa chiếc cân thăng bằng và gợi nên hình ảnh đoạn thẳng AB, đường thẳng d.
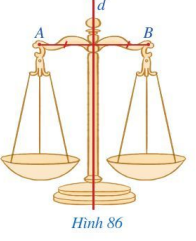
Đường thẳng d có mối liên hệ gì với đoạn thẳng AB?
Quan sát Hình 87.
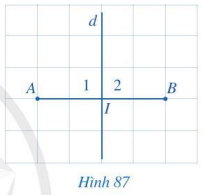
a) So sánh hai đoạn thẳng IA và IB.
b) Tìm số đo của các góc \({I_1},{I_2}\).







Danh sách bình luận