Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G(x) = 0,025{x^2}(30 - x)\), trong đó x là liều lượng thuốc được tiêm cho bênh nhân (x được tính bằng milligram). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.
Đáp án:
Đáp án:
Lập bảng biến thiên cho hàm số tính độ giảm huyết áp đó rồi tìm giá trị lớn nhất của hàm số đó.
Xét hàm số \(G(x) = 0,025{x^2}(30 - x) = 0,75{x^2} - 0,025{x^3}\); \(x \in (0; + \infty )\).
Ta có: \(G'(x) = 1,5x - 0,075{x^2} = 0 \Leftrightarrow \) x = 0 hoặc x = 20.
Bảng biến thiên:
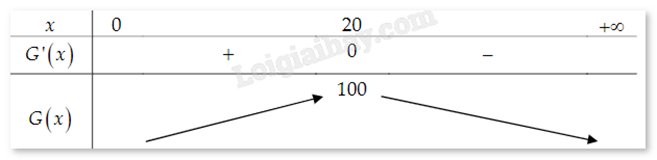
Từ bảng biến thiên, hàm G(x) đạt giá trị lớn nhất tại x = 20. Khi đó, độ giảm huyết áp là 100.

Các bài tập cùng chuyên đề
Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích \(1\;000c{m^3}\). Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/\(c{m^2}\), trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/\(c{m^2}\). Tìm các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.
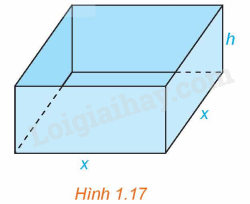
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng \(108c{m^2}\) như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Một nhà sản xuất trung bình bán được 1 000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.
a) Tìm hàm cầu.
b) Công ty nên giảm giá bao nhiêu cho người mua để doanh thu là lớn nhất?
c) Nếu hàm chi phí hằng tuần là \(C\left( x \right) = 12\;000 - 3x\) (triệu đồng), trong đó x là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán như thế nào để lợi nhuận là lớn nhất?
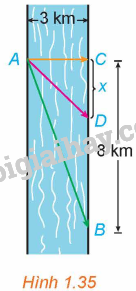
Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3km và muốn đến điểm B ở bờ đối diện cách 8km về phía hạ lưu càng nhanh càng tốt (H.1.35). Anh An có thể chèo thuyền trực tiếp qua sông đến điểm C rồi chạy bộ đến B, hoặc anh có thể chèo thuyển thẳng đến B, hoặc anh cũng có thể chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B. Nếu vận tốc chèo thuyền là 6km/h và vận tốc chạy bộ là 8km/h thì anh An phải chèo thuyền sang bờ ở điểm nào để đến B càng sớm càng tốt? (Giả sử rằng vận tốc của nước là không đáng kể so với vận tốc chèo thuyền của anh An).
Người quản lí của một khu chung cư có 100 căn hộ cho thuê nhận thấy rằng tất cả các căn hộ sẽ có người thuê nếu giá thuê một căn hộ là 8 triệu đồng một tháng. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê căn hộ thêm 100 nghìn đồng thì sẽ có thêm một căn hộ bị bỏ trống. Người quản lí nên đặt giá thuê mỗi căn hộ là bao nhiêu để doanh thu là lớn nhất?
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình 1.40. Khoảng cách từ C đến B là 4km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10km. Tổng chi phí lắp đặt cho 1km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng. Xác định vị trí điểm M trên đoạn AB (điểm nối dây từ đất liền ra đảo) để tổng chi phí lắp đặt là nhỏ nhất.

Một trang sách có dạng hình chữ nhật với diện tích là 384 cm². Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất?
Một người nông dân có 15000000 đồng để làm một hàng rào hình cữ E dọc theo một con sông bao quanh hai khu đất trông lúa có dạng hai hình chữ nhật bằng nhau (hình 35). Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60000 đồng/mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50000 đồng/ mét, mặt giáp với bờ soog không phải hàng rào. Tìm diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào.

Một bác nông dân có ba tấm lưới thép B40, mỗi tấm dài a (m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD (bờ sông là đường thẳng CD không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?

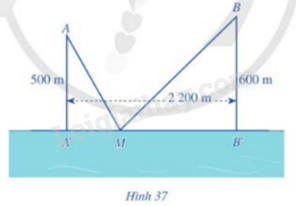
Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA’ = 500m, BB’ = 600m và người ta đo được A’B’ = 2.200m (hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B’ sao cho tổng khoảng cách từ hai xã đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
Một công ty kinh doanh bất động sản có 20 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 triệu đồng/1 tháng thì tất cả các căn hộ đều có người thuê. Nhưng cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 200 nghìn đồng/1 tháng thì có thêm một căn hộ bị bỏ trống. Hỏi công ty nên cho thuê mỗi căn hộ bao nhiêu tiền một tháng để tổng số tiền thu được là lớn nhất?
Người ta muốn chế tạo một chiếc hộp hình hộp chữ nhật có thể tích 500\(c{m^3}\) với yêu cầu dùng ít vật liệu nhất. Chiều cao hộp phải là 2 cm, các kích thước khác là x, y với x > 0 và y > 0.
a) Hãy biểu thị y theo x
b) Chứng tỏ rằng diện tích toàn phần của chiếc hộp là: \(S(x) = 500 + 4x + \frac{{1000}}{x}\)
c) Lập bảng biến thiên của hàm số S(x) trên khoảng (0; \( + \infty \)).
d) Kích thước của hộp là bao nhiêu thì dùng ít vật liệu nhất? (Làm tròn kết quả đến hàng phần mười.)

Bạn Việt muốn dùng tấm bìa hình vuông cạnh 6dm làm một chiếc hộp không nắp, có đáy là hình vuông bằng cách cắt bỏ đi 4 hình vuông nhỏ ở bốn góc của tấm bìa (Hình 11).
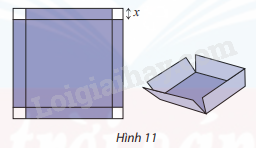
Bạn Việt muốn tìm độ dài cạnh hình vuông cần cắt bỏ để chiếc hộp đạt thể tích lớn nhất.
a) Hãy thiết lập hàm số biểu thị thể tích hộp theo x với x là độ dài cạnh hình vuông cần cắt đi.
b) Khảo sát và vẽ đồ thị hàm số tìm được. Từ đó, hãy tư vấn cho bạn Việt cách giải quyết vấn đề và giải thích vì sao cần chọn giá trị này. (Làm tròn kết quả đến hàng phần mười.)
Một lão nông chia đất cho con trai để người con canh tác riêng, biết người con sẽ được chọn miếng đất hình chữ nhật có chu vi bằng 800 m. Hỏi anh ta chọn mỗi kích thước của nó bằng bao nhiêu để diện tích canh tác lớn nhất?
-
A.
200m x 200m
-
B.
100m x 300m
-
C.
150m x 250m
-
D.
50m x 350m
Công ty A chuyên sản xuất một loại sản phẩm, ước tính rằng với q sản phẩm được sản xuất thì tổng chi phí sẽ là C(q) = 3q2 + 72q – 9789. Mỗi sản phẩm công ty sẽ bán với giá p(q) = 180 – 3q. Hãy xác định số sản phẩm công ty cần sản xuất sao cho công ty thu được lợi nhuận cao nhất.
-
A.
12
-
B.
15
-
C.
13
-
D.
9
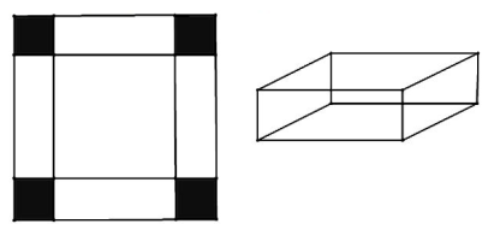
Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm, rồi gập tấm nhôm lại để được cái hộp không nắp (tham khảo hình vẽ bên). Tìm x để hộp nhận được có thể tích lớn nhất (giả thiết bề dày tấm nhôm không đáng kể).
-
A.
1
-
B.
2
-
C.
3
-
D.
4
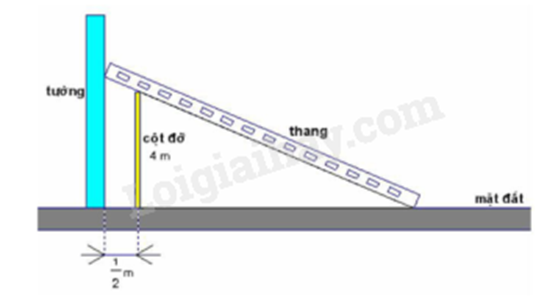
Chiều dài bé nhất của cái thang để nó có thể tựa vào tường và mặt đất, ngang qua cột đỡ cao 4 m, song song và cách tường 0,5m kể từ gốc của cột đỡ xấp xỉ số đo nào sau đây:
-
A.
5,4902
-
B.
5,602
-
C.
5,5902
-
D.
6,5902
Giả sử bạn là chủ của một xưởng cơ khí vừa nhận được một đơn đặt hàng là thiết kế một bồn chứa nước hình trụ có nắp với dung tích 20 lít. Để tốn ít nguyên vật liệu nhất, bạn sẽ chọn giá trị nào cho độ cao bồn nước trong các giá trị dưới đây?
-
A.
0,3
-
B.
0,4
-
C.
0,5
-
D.
0,6
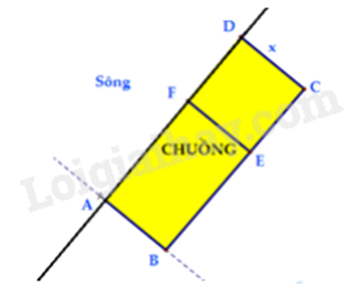
Một chủ trang trại nuôi gia cầm muốn rào thành 2 chuồng hình chữ nhật sát nhau và sát một con sông, một chuồng nuôi gà và một chuồng nuôi vịt. Biết rằng đã có sẵn 240 m hàng rào. Hỏi diện tích lớn nhất có thể bao quanh chuồng là bao nhiêu?
-
A.
1200
-
B.
2400
-
C.
3600
-
D.
4800
Khi xây nhà, chủ nhà cần làm một hồ nước bằng gạch và xi măng có dạng hình hộp đứng đáy là hình chữ nhật có chiều dài gấp ba lần chiều rộng và không nắp, có chiều cao là h và có thể tích là 18 \({m^3}\). Hãy tính chiều cao h của hồ nước sao cho chi phí xây dựng là thấp nhất?
-
A.
h = 1 m
-
B.
h = 2 m
-
C.
h = 1,5 m
-
D.
h = 2,5 m
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng (gam). Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
Cho parabol (P): \(y = {x^2}\) và điểm A(-3;0). Xác định điểm M thuộc (P) sao cho khoảng cách AM là ngắn nhất. Tung độ của điểm M bằng bao nhiêu?
Chu vi một tam giác là 16 cm, độ dài một cạnh tam giác là 6 cm. Diện tích lớn nhất của tam giác có thể đạt được là bao nhiêu?
Một tấm kẽm hình vuông ABCD có cạnh bằng 30 cm. Người ta gập tấm kẽm theo hai cạnh EF và GH cho đến khi AD và BC trùng nhau (như hình) để được một lăng trụ khuyết hai đáy.
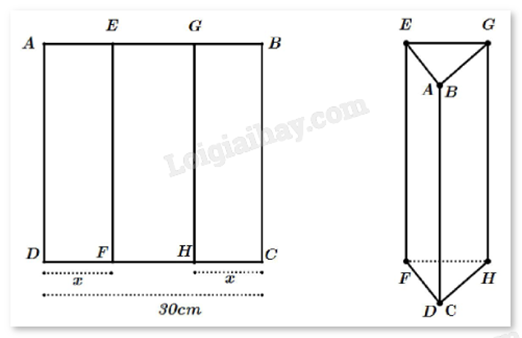
Tìm giá trị của x để thể tích khối lăng trụ lớn nhất.
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G(x) = 0,035{x^2}(15 - x)\), trong đó x là liều lượng thuốc được tiêm cho bệnh nhân (x được tính bằng milligram). Tính liều lượng thuốc cần tiêm (đơn vị milligram) cho bệnh nhân để huyết áp giảm nhiều nhất.
Một chất điểm chuyển động theo quy luật \(s(t) = 6{t^2} - {t^3}\). Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động tại giá trị lớn nhất.
Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300 km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc của cá bơi khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức \(E(v) = c{v^3}t\), trong đó c là một hằng số, E được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
Một cửa hàng bán một loại sản phẩm với lợi nhuận thu được khi bán x (trăm) sản phẩm được mô tả bởi hàm số \(L(x) = - 0,5{x^2} + 6x - 10\). Trong đó, x là số lượng sản phẩm bán ra, L(x) là lợi nhuận thu được (đơn vị: triệu đồng). Hãy xác định số lượng sản phẩm mà cửa hàng cần bán ra để lợi nhuận đạt mức cao nhất.
Nồng độ \(C\) của một loại hoá chất trong máu sau \(t\) giờ tiêm vào cơ thể được cho bởi công thức: \(C\left( t \right) = \frac{{3t}}{{27 + {t^3}}}\) với \(t \ge 0\) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
Sau khoảng bao nhiêu giờ tiêm thì nồng độ của hoá chất trong máu là cao nhất?
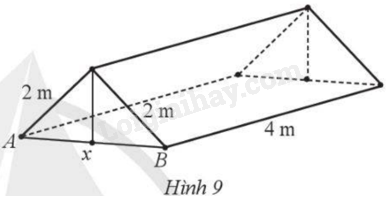
Nhóm bạn Đức dựng trên một khu đất bằng phẳng một chiếc lều từ một tấm bạt hình vuông có độ dài cạnh 4 m như Hình 9 với hai mép tấm bạt sát mặt đất. Tính khoảng cách \(AB\) để khoảng không gian trong lều là lớn nhất.