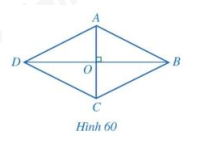
Hình 3.73 cho ta hình ảnh của một chiếc thang nâng thủy lực với khung nâng được lắp đặt từ các thanh giàn bằng nhau, gắn với nhau ở hai đầu và trung điểm mỗi thanh.
a) Tứ giác \(CKDM\) và tứ giác \(ABCD\) là hình gì?
b) Vì sao các đường thẳng \(AB,CD,EF\) và \(GH\) luôn song song với nhau? Vì sao các điểm \(I,K,M,N,O\) luôn thẳng hàng?
c) Tính chiều cao \(OI\) của thang khi \(AB = 1,6m\) và \(AD = 2m\)
Dựa vào tính chất hình bình hành và tính chất hình chữ nhật để xác định.
c) Sử dụng định lí Pythagore để tính độ dài BD, từ đó tính OI.
a) Xét tứ giác \(CKDM\), ta có:
\(CM = MD = DK = KC\) (vì các thanh giàn bằng nhau và cắt nhau tại trung điểm)
Suy ra tứ giác \(CKDM\) là hình thoi.
Xét tứ giác \(ABCD\), ta có:
\(AD = CB\)
Mà \(AD\) và \(CB\) là hai đường chéo
nên \(ABCD\) là hình chữ nhật.
b) Các đường thẳng \(AB,CD,EF\) và \(GH\) luôn song song với nhau vì các đường thẳng này luôn bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Các điểm \(I,K,M,N,O\) luôn thẳng hàng vì các điểm này đều là giao điểm của hai đường chéo hình bình hành.
c) Vì ABCD là hình chữ nhật nên \(AB \bot BD\) do đó tam giác ABD vuông tại B.
Áp dụng định lí Pythagore vào tam giác ABD, ta có:
\(BD^2 = AD^2 - AB^2 = 2^2 – 1,6^2 = 1,44\) nên \(BD = 1,2 (m)\)
Ta dễ dàng chứng minh được tứ giác CDFE, EFHG là hình chữ nhật và BD = DF = FH
Khi đó BD = DF = HF = 1,2m
Mà OI = HB = BD + DF + FH = 1,2 + 1,2 + 1,2 = 3,6 (m)
Vậy OI = 3,6m.
Các bài tập cùng chuyên đề
Hãy viết giả thiết, kết luận của câu c trong Định lí 2.
Trong Hình 3.51, hình nào là hình thoi? Vì sao?
Cho \(ABCD\) là một hình bình hành. Giải thích tại sao tứ giác \(ABCD\) có bốn cạnh bằng nhau trong mỗi trường hợp sau:
Trường hợp 1: \(AB = AD\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là phân giác góc \(BAD\)
Trường hợp 4: \(BD\) là phân giác góc \(ABC\)
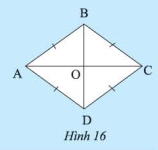
Quan sát hình 21. Chứng minh rằng tứ giác \(EFGH\) là hình thoi.
a) Cho hình bình hành ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình thoi hay không?
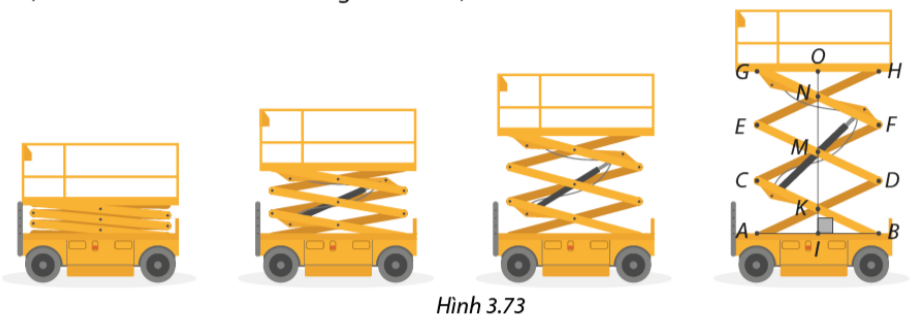
b) Cho hình bình hành ABCD có hai đường chéo AC và BD vuông góc với nhau (hình 60)
- Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?
ABCD có phải là hình thoi hay không?
Cho tam giác ABC cân tại A có M là trung điểm BC. Trên tia đối của tia MA lấy điểm N sao cho MN = MA. Chứng minh tứ giác ABNC là hình thoi.
Cho hình bình hành ABCD có tia AC là tia phân giác của góc DAB. Chứng minh ABCD là hình thoi.
Cho hình chữ nhật ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác MNPQ là hình thoi.
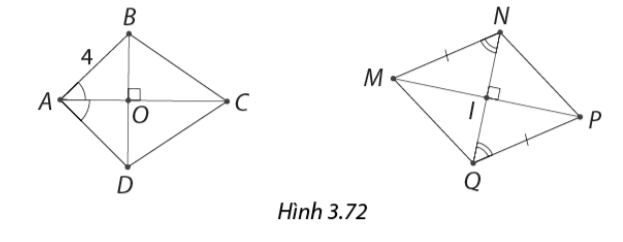
Tứ giác nào trong Hình 3.72 là hình thoi?
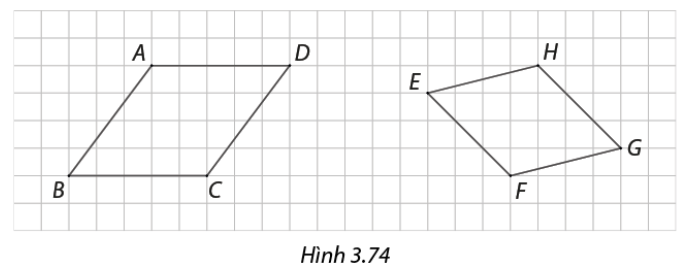
Trong Hình 3.74, tứ giác nào là hình thoi?
Cho hình vuông ABCD. Trên cạnh BC lấy điểm N. Từ A kẻ đường thẳng vuông góc với AN cắt đường thẳng CD tại Q. Gọi I là trung điểm của NQ. Gọi M là giao điểm AI và CD. Qua N dựng đường thẳng song song với CD cắt AI tại P. Chứng minh rằng:
a) ∆PIN = ∆MIQ.
b) Tứ giác MNPQ là hình thoi.
Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi.
Gọi O là giao điểm của hai đường chéo hình bình hành ABCD. Với mỗi tam giác OAB, OBC, OCD, ODA, xét giao điểm ba đường phân giác của tam giác đó. Tại sao bốn điểm vừa vẽ là bốn đỉnh của một hình thoi?
Trong các câu sau, câu nào đúng?
A. Tứ giác có các góc đối bằng nhau là hình thoi.
B. Tứ giác có hai đường chéo vuông góc là hình thoi.
C. Hình thang có các đường chéo bằng nhau là hình thoi.
D. Hình bình hành có các đường chéo vuông góc là hình thoi.
Cho tam giác \(ABC\) nhọn có các đường cao \(BD,CE\). Tia phân giác của các góc \(ACE,ABD\) cắt nhau tại \(O\) và cắt \(AB,AC\) lần lượt tại \(M,N\). Tia \(BN\) cắt \(CE\) tại \(K\), tia \(CM\) cắt \(BD\) tại \(H\). Chứng minh:
a) \(BN \bot CM\)
b) Tứ giác \(MNHK\) là hình thoi.
Cho \(ΔABC\) cân tại \(A\) đường trung tuyến \(AH\). Gọi \(I\) và \(K\) lần lượt là trung điểm của \(AC\) và \(AB\). Gọi \(E\) là điểm sao cho \(I\) là trung điểm của \(HE\). Giải thích tại sao tứ giác \(AKHI\) là hình thoi.
Khẳng định nào sau đây là sai?
Khẳng định nào sau đây là sai?
Cho tam giác \(ABC\) vuông ở \(A\), trung tuyến \(AM\). Gọi \(D\) là trung điểm của \(AB\) và \(MD\parallel AC\), \(M’\) là điểm đối xứng với \(M\) qua \(D\). Tứ giác \(AMBM’\) là hình gì?
Cho hình thang cân \(MNPQ\). Gọi \(A\), \(B\), \(C\), \(D\) lần lượt là các điểm thuộc các cạnh \(MN\), \(NP\), \(PQ\), \(QM\) và \(AD = \frac{1}{2}QN\), \(BC = \frac{1}{2}QN\), \(AB = \frac{1}{2}MP\), \(DC = \frac{1}{2}MP\). Tứ giác \(ABCD\) là hình gì?
Cho hình thang \(ABCD\). Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là các điểm thuộc các cạnh \(AB\), \(BC\), \(CD\), \(DA\) và \(MN\parallel AC\), \(MN = \frac{1}{2}AC\), \(PQ\parallel AC\), \(PQ = \frac{1}{2}AC\), \(MQ = \frac{1}{2}BD\). Hình thang \(ABCD\) có thêm điều kiện nào dưới đây thì \(MNPQ\) là hình thoi?
Cho hình thoi \(ABCD\). Trên các cạnh \(BC\) và \(CD\) lần lượt lấy hai điểm \(E\) và \(F\) sao cho \(BE = DF\). Gọi \(G\), \(H\) thứ tự là giao điểm của \(AE\), \(AF\) với đường chéo \(DB\). Tứ giác \(AGCH\) là hình gì?
Cho hình bình hành \(ABCD\). Gọi \(E, F\) lần lượt là trung điểm của \(AD, BC\). Các đường \(BE, DF\) cắt \(AC\) tại \(P, Q\). Tứ giác \(EPFQ\) là hình thoi nếu \(\widehat {ACD}\) bằng
Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB và MD // AC, \({M'}\) là điểm đối xứng với M qua D. Tứ giác \(AMBM'\) là hình gì?
