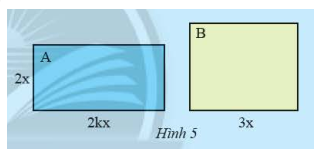
Hình chữ nhật \(A\) có chiều rộng \(2x\) (cm), chiều dài gấp \(k\) (\(k > 1\) lần chiều rộng. Hình chữ nhật \(B\) có chiều dài \(3x\) (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì \(B\) phải có chiều rộng bằng bao nhiêu?
Áp dụng công thức tính diện tích hình chữ nhật.
Áp dụng quy tắc nhân đơn thức với đơn thức, chia đơn thức cho đơn thức.
Diện tích hình chữ nhật \(A\) là: \(2kx.2x = 4k{x^2}\) \(c{m^2}\)
Muốn hai hình chữ nhật \(A\) và \(B\) có diện tích bằng nhau thì chiều rộng hình chữ nhật \(B\) là:
\(4k{x^2}:\left( {3x} \right) = \left( {4:3} \right).\left( {{x^2}:x} \right).k = \frac{4}{3}xk\) (cm)
Các bài tập cùng chuyên đề
Rút gọn biểu thức: \(\left( {3{x^2} - 5xy - 4{y^2}} \right).\left( {2{x^2} + {y^2}} \right) + \left( {2{x^4}y - {x^3}{y^3} - {x^2}{y^4}} \right):\left( {\dfrac{1}{5}xy} \right)\)
a) Tìm đơn thức C nếu \(5x{y^2}.C = 10{x^3}{y^3}\)
b) Với đơn thức C tìm được ở câu a, hãy tìm đơn thức K sao cho \(\left( {K + 5x{y^2}} \right).C = 6{x^4}y + 10{x^3}{y^3}\)
Chuyện rằng Rùa chạy đua với Thỏ. Thỏ chạy nhanh gấp 60 lần Rùa, nhưng chỉ sau t phút chạy, Thỏ đã dừng lại mặc dù chưa đến đích. Do mải chơi, Thỏ không biết rằng Rùa vẫn cần mẫn chạy liên tục trong 90t phút và đến đích trước Thỏ.
a) Gọi v (m/phút) là vận tốc chạy của Rùa. Hãy viết đơn thức biểu thị quãng đường mà Thỏ và Rùa đã chạy.
b) Hỏi Rùa đã chạy được quãng đường dài gấp bao nhiêu lần quãng đường Thỏ đã chạy?
Trên một dòng sông, để đi được \(10\)km, một chiếc xuồng tiêu tốn \(a\) lít dầu khi xuôi dòng và tiêu tốn \(\left( {a + 2} \right)\) lít dầu khi ngược dòng. Viết biểu thức biểu thị số lít dầu mà xuồng tiêu tốn để đi từ bến A ngược dòng đến bến B, rồi quay lại bến A. Biết khoảng cách giữa hai bến là \(b\) km.
Thực hiện các phép tính sau:
a) \(\dfrac{{8y}}{{3{x^2}}} \cdot \dfrac{{9{x^2}}}{{4{y^2}}}\)
b) \(\dfrac{{3x + {x^2}}}{{{x^2} + x + 1}} \cdot \dfrac{{3{x^3} - 3}}{{x + 3}}\)
c) \(\dfrac{{2{x^2} + 4}}{{x - 3}} \cdot \dfrac{{3x + 1}}{{x - 1}}:\dfrac{{{x^2} + 2}}{{6 - 2x}}\)
d) \(\dfrac{{2{x^2}}}{{3{y^3}}}:\left( { - \dfrac{{4{x^3}}}{{21{y^2}}}} \right)\)
e) \(\dfrac{{2x + 10}}{{{x^3} - 64}}:\dfrac{{{{\left( {x + 5} \right)}^2}}}{{2x - 8}}\)
g) \(\dfrac{1}{{x + y}}\left( {\dfrac{{x + y}}{{xy}} - x - y} \right) - \dfrac{1}{{{x^2}}}:\dfrac{y}{x}\)
Thực hiện phép tính:
a) \(\left( { - xy} \right)\left( { - 2{{\rm{x}}^2}y + 3{\rm{x}}y - 7{\rm{x}}} \right)\)
b) \(\left( {\dfrac{1}{6}{x^2}{y^2}} \right)\left( { - 0,3{{\rm{x}}^2}y - 0,4{\rm{x}}y + 1} \right)\)
c) \(\left( {x + y} \right)\left( {{x^2} + 2{\rm{x}}y + {y^2}} \right)\)
d) \(\left( {x - y} \right)\left( {{x^2} - 2{\rm{x}}y + {y^2}} \right)\)
Thực hiện phép tính:
a) \(\left( {39{{\rm{x}}^5}{y^7}} \right):\left( {13{{\rm{x}}^2}y} \right)\)
b) \(\left( {{x^2}{y^2} + \dfrac{1}{6}{x^3}{y^2} - {x^5}{y^4}} \right):\left( {\dfrac{1}{2}x{y^2}} \right)\)
Rút gọn biểu thức:
\(a)\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\)
b) \(\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)\)
c) \(\left( {4{\rm{x}} - 1} \right)\left( {6y + 1} \right) - 3{\rm{x}}\left( {8y + \dfrac{4}{3}} \right)\)
d) \(\left( {x + y} \right)\left( {x - y} \right) + \left( {x{y^4} - {x^3}{y^2}} \right):\left( {x{y^2}} \right)\)
a) Chứng minh rằng biểu thức \(P = 5{\rm{x}}\left( {2 - x} \right) - \left( {x + 1} \right)\left( {x + 9} \right)\) luôn nhận giá trị âm với mọi giá trị của biến x.
b) Chứng minh rằng biểu thức \(Q = 3{{\rm{x}}^2} + x\left( {x - 4y} \right) - 2{\rm{x}}\left( {6 - 2y} \right) + 12{\rm{x}} + 1\) luôn nhận giá trị dương với mọi giá trị của biến x và y
Rút gọn biểu thức:
a) \(A = \left( {9{x^2} - 6xy + 4{y^2} + 1} \right)\left( {3x + 2y} \right) - \left( {3{x^5}y + \frac{8}{9}{x^2}{y^4} - {x^3}y} \right):\frac{1}{9}{x^2}y\);
b) \(B = \left( {5{x^3}{y^2} - 4{x^2}{y^3}} \right):2{x^2}{y^2} + \left( {3{x^4} + 6x{y^2}} \right):3xy - x\left( {{x^2} - 0,5} \right)\).
a) Tìm đơn thức M, biết rằng \(\frac{7}{3}{x^3}{y^2}:M = 7x{y^2}\) .
b) Tìm đơn thức N sao cho \(N:0,5x{y^2}z = - xy\) .
Rút gọn biểu thức \((3{x^2}\;-5xy-4{y^2}).(2{x^2}\; + {y^2}) + (2{x^4}{y^2}\; + {x^3}{y^3}\; + {x^2}{y^4}):\;\left( {\frac{1}{5}xy} \right).\)
Chuyện rằng Rùa chạy đua với Thỏ. Thỏ chạy nhanh gấp 60 lần rùa, nhưng chỉ sau t phút chạy, Thỏ đã dừng lại mặc dù chưa đến đích. Do mải chơi, Thỏ không biết rằng Rùa vẫn cần mẫn chạy liên tục trong 90t phút và đến đích trước Thỏ.
a) Gọi v (m/phút) là vận tốc chạy của Rùa. Hãy viết các đơn thức biểu thị quãng đường mà Thỏ và Rùa đã chạy.
b) Hỏi Rùa đã chạy được quãng đường dài gấp bao nhiêu lần quãng đường Thỏ đã chạy?
Tìm đơn thức E, biết rằng \(\left( {6{x^2}{y^3}\;-E} \right):2xy = 3x{y^2}\; + \;\;\frac{1}{3}{x^2}y\).
Thực hiện phép tính:
a) \( - \frac{1}{3}xy\left( {3{x^3}{y^2} - 6{x^2} + {y^2}} \right)\);
b) \(\left( {9{x^2}{y^4}z - 12{x^3}{y^2}{z^4} - 4x{y^3}{z^2}} \right):xyz\).
Thu gọn biểu thức:
a) \(\left( { - 9{x^2}{y^3} + 6{x^3}{y^2} - 4x{y^2}} \right):3x{y^2};\)
b) \(\frac{1}{2}xy\left( {{x^5} - {y^3}} \right) - {x^2}y\left( {\frac{1}{4}{x^4} - {y^3}} \right).\)
Thu gọn biểu thức:
a) \(\left( {30{x^4}{y^3} - 25{x^2}{y^3} - 3{x^4}{y^4}} \right):5{x^2}{y^3};\)
b) \({x^3}{y^4}\left( {{x^2} - 2{y^3}} \right) - 2{x^3}{y^3}\left( {{x^4} - {y^4}} \right).\)
Thực hiện phép tính:
a) \({\left( {2x + 3} \right)^2}\);
b) \((15{x^4}{y^5} - 30{x^3}{y^4} + 5{x^5}{y^4}):(5{x^3}{y^3})\);
c) \(\left( {x + 3} \right)\left( {{x^2} + 3x - 5} \right)\).
