Quan sát đồ thị của hàm số \(y = f\left( x \right) = {x^3}--3{x^2} + 1{\rm{ }}\) trong Hình 5.
a) Tìm khoảng (a; b) chứa điểm x = 0 mà trên đó f(x) < f(0) với mọi \(x \ne 0\).
b) Tìm khoảng (a; b) chứa điểm x = 2 mà trên đó f(x) > f(2) với mọi \(x \ne 2\).
c) Tồn tại hay không khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi \(x \ne 1\) hoặc f(x) < f(1) với mọi \(x \ne 1\)?
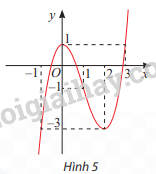
Quan sát đồ thị
a) Trên khoảng (-1; 2), f(x) < f(0) với mọi \(x \ne 0\)
b) Trên khoảng (0; 3), f(x) > f(2) với mọi \(x \ne 2\)
c) Không tồn tại khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi \(x \ne 1\) hoặc f(x) < f(1) với mọi \(x \ne 1\)

Các bài tập cùng chuyên đề
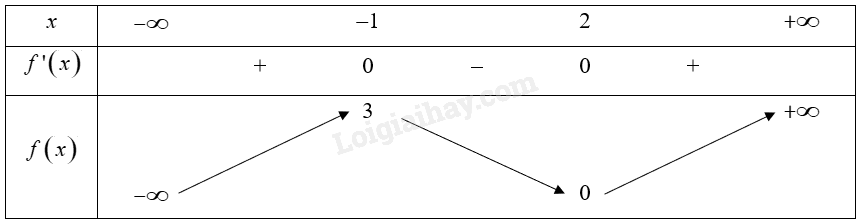
Giải thích vì sao nếu f’(x) không đổi dấu qua \({x_0}\) thì \({x_0}\) không phải là điểm cực trị của hàm số f(x)?
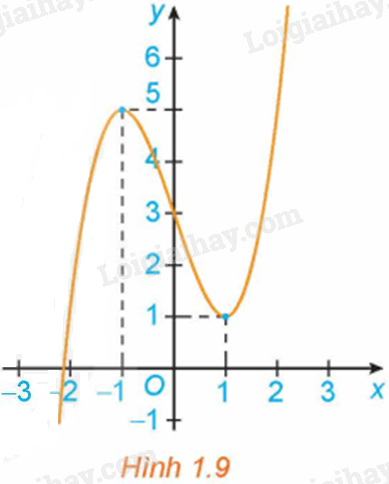
Hình 1.9 là đồ thị của hàm số \(y = f\left( x \right)\). Hãy tìm các cực trị của hàm số.
Cho hàm số \(y = f\left( x \right) = \left| x \right|\).
a) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\) và \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\). Từ đó suy ra hàm số không có đạo hàm tại \(x = 0\).
b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại \(x = 0\). (Xem Hình 1.4)
Quan sát bảng biến thiên dưới đây và cho biết:
a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) hay không.
b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\) hay không.

Dựa vào đồ thị hàm số \(y = f\left( x \right) = - {x^3} - 3{x^2} + 3\) ở Hình 3, hãy so sánh:
a) \(f\left( { - 2} \right)\) với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).
b) \(f\left( 0 \right)\)với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).

Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng:
a) \(2\).
b) \(3\).
c) \( - 4\).
d) \(0\).
Đồ thị của hàm số \(y = \left\{ \begin{array}{l}{x^2}{\rm{ }}khi{\rm{ }}x \le 1{\rm{ }}\\2 - x{\rm{ }}khi{\rm{ }}x > 1\end{array} \right.\) được cho ở Hình 9.

a) Tìm điểm cực đại và điểm cực tiểu của hàm số.
b) Tại x = 1, hàm số có đạo hàm không?
c) Thay mỗi dấu ? bằng kí hiệu (+, –) thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu của y' khi x đi qua điểm cực đại và điểm cực tiểu.
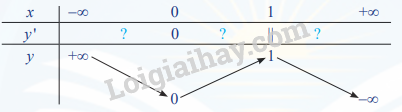
Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8
Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số đạt cực đại tại

A. x = 0. B. x = 3. C. x = 4. D. x = 5.
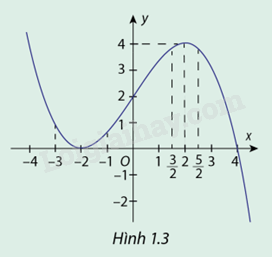
Hàm số \(y = f(x) = - \frac{1}{8}{x^3} + \frac{3}{2}x + 2\) có đồ thị cho ở hình 1.3
a) Giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị, só sánh \(f( - 2)\) với các giá trị khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, só sánh \(f(2)\) với các giá trị khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và bảng xét dấu của đạo hàm như sau:

Số điểm cực trị của hàm số đã cho là:
A. 0.
B. 1.
C. 2.
D. 3.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho là:
A. ‒1.
B. 3.
C. 2.
D. 0.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
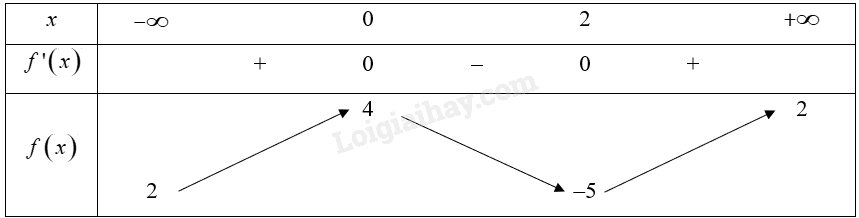
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại \(x = - 5\).
B. Hàm số có giá trị cực đại bằng 0.
C. Hàm số đạt cực tiểu tại \(x = 2\).
D. Hàm số đạt cực đại tại \(x = 4\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 5. Số điểm cực trị của hàm số đã cho là:
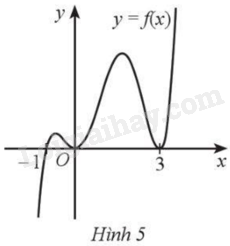
A. 2.
B. 4.
C. 1.
D. 3.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 6. Giá trị cực tiểu của hàm số đã cho là:
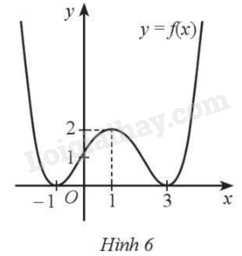
A. 2.
B. 1.
C. ‒1.
D. 0.
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
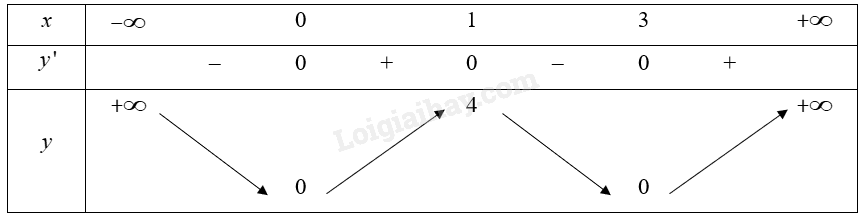
Số điểm cực trị của hàm số là:
A. 0.
B. 1.
C. 2.
D. 3.
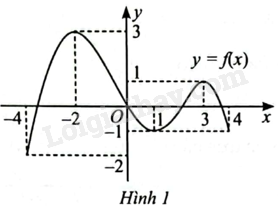
Hàm số \(y = f\left( x \right)\) trong Hình 1 có bao nhiêu điểm cực trị?
A. 2.
B. 3.
C. 4.
D. 5.
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì
-
A.
${x_0}$ là điểm cực đại của hàm số.
-
B.
${x_0}$ là điểm cực tiểu của hàm số.
-
C.
${x_0}$ là điểm cực đại của đồ thị hàm số.
-
D.
${x_0}$ là điểm cực tiểu của đồ thị hàm số.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\left( {a;b} \right)\). Nếu \(f'\left( x \right)\) đổi dấu từ dương sang âm qua điểm \({x_0}\) thì:
-
A.
\({x_0}\) là điểm cực đại của hàm số
-
B.
\({x_0}\) là điểm cực tiểu của hàm số.
-
C.
\({x_0}\) là điểm cực đại của đồ thị hàm số
-
D.
\({x_0}\) là điểm cực tiểu của đồ thị hàm số.
Cho hàm số f(x) có đạo hàm \(f'(x) = x{(x + 1)^2}{(x - 2)^3}\), \(\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Cho hàm số y = f(x) có đồ thị như hình vẽ. Hàm số đạt cực tiểu tại
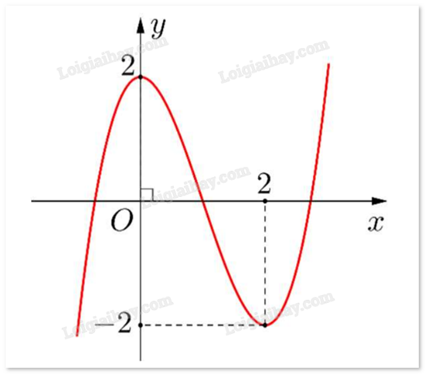
-
A.
\(x = 2\)
-
B.
\(x = - 2\)
-
C.
\(x = 0\)
-
D.
\(x = \pm 2\)
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ.
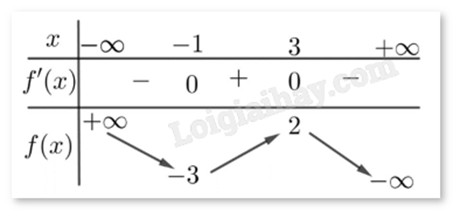
Điểm cực đại của hàm số đã cho là
-
A.
\(x = 3\)
-
B.
\(x = - 1\)
-
C.
\(x = 2\)
-
D.
\(x = - 3\)
Cho hàm số f(x) có đồ thị y = f’(x) như hình.
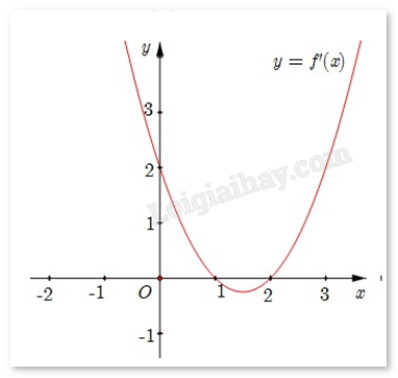
Hàm số f(x) có cực tiểu là
-
A.
x = 2
-
B.
x = 1
-
C.
x = 0
-
D.
Đáp án khác
Cho hàm số y = f(x) có đồ thị như hình vẽ.
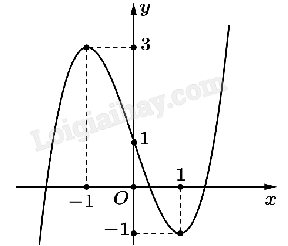
Điểm cực đại của hàm số đã cho là
-
A.
\(x = 3\)
-
B.
\(x = - 1\)
-
C.
\(x = 1\)
-
D.
\(x = 0\)
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ.
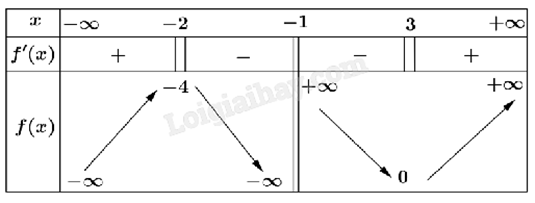
Điểm cực đại của hàm số đã cho là
-
A.
\(x = 3\)
-
B.
\(x = - 1\)
-
C.
\(x = - 2\)
-
D.
\(x = - 4\)
Cho hàm số f(x) liên tục trên \(\mathbb{R}\) và có bảng xét dấu f’(x) như sau:
Số điểm cực đại của hàm số đã cho là
-
A.
4
-
B.
2
-
C.
3
-
D.
0
Cho hàm số f(x) có bảng biến thiên như sau:
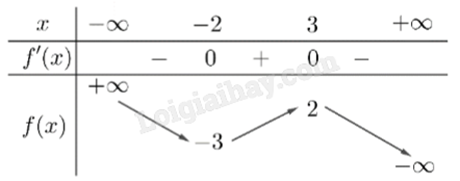
Giá trị cực đại của hàm số đã cho bằng
-
A.
3
-
B.
2
-
C.
-2
-
D.
-3
Cho hàm số y = f(x) liên tục trên và có bảng xét dấu của f’(x) như hình dưới:
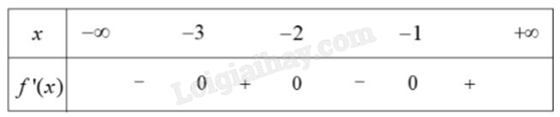
Hàm số y = f(x) có bao nhiêu điểm cực trị?
-
A.
1
-
B.
2
-
C.
4
-
D.
3
Cho hàm số bậc ba có bảng biến thiên như hình vẽ dưới đây.

Giá trị cực tiểu của hàm số là
-
A.
2
-
B.
1
-
C.
-1
-
D.
-2
Cho hàm số y = f(x) liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình dưới.
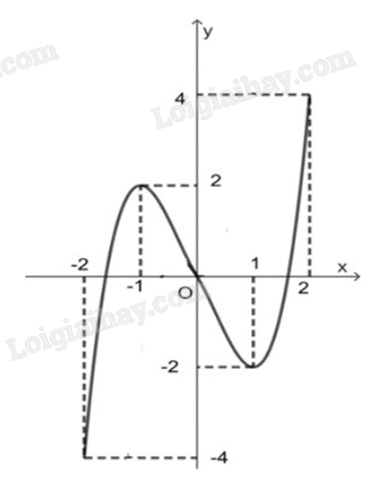
Hàm số y = f(x) đạt cực tiểu tại điểm
-
A.
x = -2
-
B.
x = -1
-
C.
x = 1
-
D.
x = 0






