Cho tam giác ABC có đương tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm; BP = 3 cm; CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.
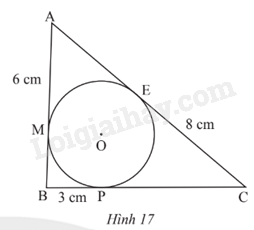
- Dựa vào tính chất hai tiếp tuyến cắt nhau để chứng minh BM = BP, AM = AE, CE = CP.
- Tính chu vi tam giác bằng AB + AC + BC.
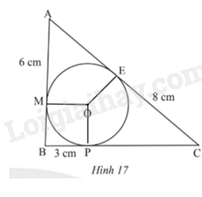
Ta có MB và BP là hai tiếp tuyến tại M và P của đường tròn (O) và cắt nhau tại B.
Do đó: BM = BP = 3cm (Tính chất hai tiếp tuyến cắt nhau).
Ta có AM và AE là hai tiếp tuyến tại M và E của đường tròn (O) và cắt nhau tại A.
Do đó: AM = AE = 6cm (Tính chất hai tiếp tuyến cắt nhau).
Ta có CE và CP là hai tiếp tuyến tại E và P của đường tròn (O) và cắt nhau tại C.
Do đó: CE = CP = 8cm (Tính chất hai tiếp tuyến cắt nhau).
Suy ra chu vi tam giác ABC là:
AB + AC + BC = (AM + MB) + (AE + EC) + (BP + PC)
= (6 + 3) + (6 + 8) + (3 + 8) = 34 cm.

Các bài tập cùng chuyên đề
Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai?
-
A.
Khoảng cách từ điểm đó đến hai tiếp điểm là bằng nhau
-
B.
Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai bán kính
-
C.
Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi hai bán kính
-
D.
Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi tiếp tuyến
(Dựa vào hình vẽ có được sau HĐ3).
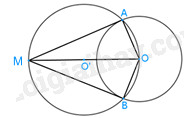
Bằng cách xét hai tam giác OMA và OMB, chứng minh rằng:
a) MA = MB;
b) MO là tia phân giác của góc AMB;
c) OM là tia phân giác của góc AOB.
Cho góc xMy và điểm A thuộc tia Mx. Hãy vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xMy sao cho A là một trong hai tiếp điểm.
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.
a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB.
b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.
Cho đường tròn O và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10).
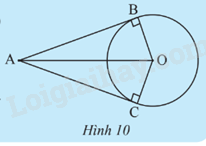
a) Chứng minh hai tam giác ABO và ACO bằng nhau.
b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.
Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F. Cho biết \(\widehat {EMF} = {60^o}\).
a) Tính số đo \(\widehat {EMI}\) và \(\widehat {EIF}\) .
b) Tính độ dài MI.
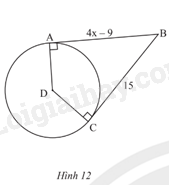
Tìm giá trị x trong Hình 12.
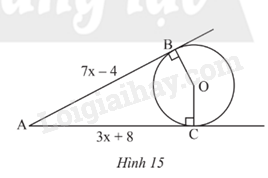
Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x.
Cho đường tròn (O) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) thoả mãn \(\widehat {AMB} = {60^o}\). Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.
Cho đường tròn \(\left( {O;R} \right)\). Các đường thẳng \(c,d\) lần lượt tiếp xúc với đường tròn \(\left( {O;R} \right)\) tại \(A,B\) và cắt nhau tại \(M\) (Hình 38).
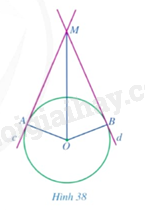
a) Các tam giác \(MOA\) và \(MOB\) có bằng nhau hay không?
b) Hai đoạn thẳng \(MA\) và \(MB\) có bằng nhau hay không?
c) Tia \(MO\) có phải là tia phân giác của góc \(AMB\) hay không?
d) Tia \(OM\) có phải là tia phân giác của góc \(AOB\) hay không?
Cho đường tròn \(\left( {O;R} \right)\) và điểm \(M\) nằm ngoài đường tròn. Hai đường thẳng \(c,d\) qua \(M\) lần lượt tiếp xúc với \(\left( O \right)\) tại \(A,B\) biết \(\widehat {AMB} = 120^\circ \). Chứng minh \(AB = R\).
Ròng rọc là một loại máy cơ đơn giản có rãnh và có thể quay quanh một trục, được sử dụng rộng rãi trong công việc nâng lên và hạ xuống vật nặng trong cuộc sống. Trong Hình 41a, có một sợi dây không dãn vắt qua ròng rọc.
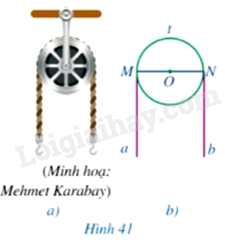
Giả sử ròng rọc được minh họa bởi đường tròn \(\left( O \right)\), sợi dây vắt qua ròng rọc được minh hoạ bởi cung \(MtN\) và hai tiếp tuyến \(Ma,Nb\) của đường tròn \(\left( O \right)\) (Hình 41b). Chứng minh \(Ma//Nb\).
Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài đường tròn. Hai đường thẳng thẳng \(c,d\) đi qua \(M\) lần lượt tiếp xúc với \(\left( O \right)\) tại \(A,B\). Tia phân giác của góc \(MAB\) cắt \(MO\) tại \(I\). Chứng minh điểm \(I\) cách đều ba đường thẳng \(MA,MB\) và \(AB\).
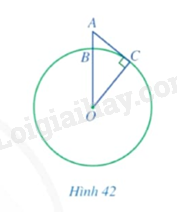
Một người quan sát đặt mắt ở vị trí \(A\) có độ cao cách mực nước biển là \(AB = 5m\). Cắt bề mặt Trái Đất bởi một mặt phẳng đi qua điểm \(A\) và tâm của Trái Đất thì phần chung giữa chúng là một đường tròn lớn tâm \(O\) như Hình 42. Tầm quan sát tối đa từ vị trí \(A\) là đoạn \(AC\), trong đó \(C\) là tiếp điểm của tiếp tuyến đi qua \(A\) với đường tròn \(\left( O \right)\). Tính độ dài đoạn thẳng \(AC\) (theo đơn vị kilômét và làm tròn kết quả đến hàng phần mười), biết bán kính Trái Đất là: \(OB = OC \approx 6400km\).
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB\) và các đường thẳng \(m,n,p\) lần lượt tiếp xúc với đường tròn tại \(A,B,C\) (Hình 43).
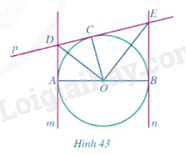
Chứng minh:
a) \(AD + BE = DE\);
b) \(\widehat {COD} = \frac{1}{2}\widehat {COA}\) và \(\widehat {COE} = \frac{1}{2}\widehat {COB}\);
c) Tam giác \(ODE\) vuông;
d) \(\frac{{OD.OE}}{{DE}} = R\).
Cho hai đường tròn \(\left( {I;r} \right)\) và \(\left( {K;R} \right)\) tiếp xúc ngoài với nhau tại \(P\) với \(R \ne r\), đường thẳng \(a\) lần lượt tiếp xúc với \(\left( {I;r} \right)\) và \(\left( {K;R} \right)\) tại \(A\) và \(B,a\) cắt \(KI\) tại \(O\). Đường thẳng qua \(P\) vuông góc với \(IK\) cắt đường thẳng \(a\) tại \(M\). Chứng minh:
a) \(\frac{{OI}}{{OK}} = \frac{r}{R}\);
b) \(AB = 2MP\);
c) \(\widehat {IMK} = 90^\circ \).
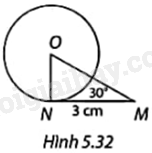
Trong Hình 5.32, MN là tiếp tuyến của đường tròn (O; R) tại N. Tính R.
Vẽ đường tròn (O) và lấy hai điểm A, B thuộc (O) (AB không là đường kính). Vẽ tiếp tuyến tại A và B cắt nhau tại M. Em hãy đo và so sánh:
a) MA và MB;
b) \(\widehat {AMO}\) và \(\widehat {BMO}\);
c) \(\widehat {AOM}\) và \(\widehat {BOM}\).
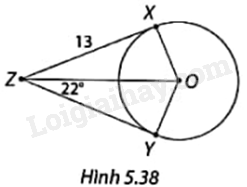
Trong Hình 5.38, ZX và ZY là hai tiếp tuyến của đường tròn tâm O với tiếp điểm lần lượt là X và Y. Xác định số đo \(\widehat {XOY}\) và độ dài YZ.
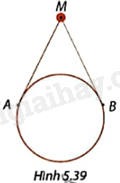
Trong Hình 5.39, người ta dùng một đoạn dây gắn vào hai điểm A, B trên viền một chiếc gương tròn để treo gương vào điểm M. Biết tổng độ dài dây là 82cm, \(\widehat {AMB} = {52^o}\) và MA, MB tiếp xúc với viền gương. Tính đường kính của gương. Làm tròn kết quả đến đơn vị centimét.
Từ điểm M nằm ngoài đường tròn (O; 5cm), \(MO = 13cm\), vẽ hai tiếp tuyến MA, MB (A, B là các tiếp điểm).
a) Tính độ dài MA và MB.
b) Cho C là điểm bất kì thuộc đường tròn (O) và nằm trong góc AOB. Tiếp tuyến tại C của đường tròn cắt MA tại N và cắt MB tại P. Tính chu vi \(\Delta MNP\).
Cho MA và MB là hai tiếp tuyến của đường tròn (O; R) (A, B là hai tiếp điểm) sao cho \(\Delta \)MAB là tam giác đều. Khoảng cách OM bằng
A. \(\frac{1}{2}R\).
B. R.
C. 2R.
D. \(R\sqrt 2 \).
“Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi… Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi…” Hai cụm từ thích hợp vào chỗ trống lần lượt là
-
A.
hai tiếp tuyến, hai bán kính đi qua tiếp điểm
-
B.
hai bán kính đi qua tiếp điểm, hai tiếp tuyến
-
C.
hai tiếp tuyến, hai dây cung
-
D.
hai dây cung, hai bán kính
Hai tiếp tuyến tại $B$ và $C$ của đường tròn $\left( O \right)$ cắt nhau tại$A$ .
Hai tiếp tuyến tại \(B\) và \(C\) của đường tròn \(\left( O \right)\) cắt nhau tại \(A.\) Biết \(OB = 3cm;\,OA = 5cm.\)
Cho hai tiếp tuyến tại $A$ và $B$ của đường tròn \(\left( O \right)\) cắt nhau tại M, biết \(\widehat {AMB} = {50^0}\) .
Cho hai tiếp tuyến tại $C$ và $D$ của đường tròn \(\left( O \right)\) cắt nhau tại M, biết \(\widehat {CND} = {60^0}\) .
Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Trên AO lấy điểm M sao cho \(AM = AB.\) Các tia BM và CM lần lượt cắt đường tròn tại một điểm thứ hai là D và E. Chọn câu đúng.
-
A.
M là tâm đường tròn ngoại tiếp tam giác OBC
-
B.
DE là đường kính của đường tròn (O)
-
C.
M là tâm đường tròn nội tiếp tam giác OBC
-
D.
Cả A, B, C đều sai
Hai tiếp tuyến tại $A$ và $B$ của đường tròn $(O)$ cắt nhau tại $I$ . Đường thẳng qua $I$ và vuông góc với $IA$ cắt $OB$ tại $K$. Chọn khẳng định đúng.
-
A.
$OI = OK = KI$
-
B.
$KI = KO$
-
C.
$OI = OK$
-
D.
$IO = IK$
Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${120^0}$. Biết chu vi tam giác $MAB$ là $6\left( {3 + 2\sqrt 3 } \right)cm$, tính độ dài dây $AB.$
-
A.
$18\,cm$
-
B.
$6\sqrt 3 cm$
-
C.
$12\sqrt 3 \,cm$
-
D.
$15\,cm$







Danh sách bình luận