a) Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng a (Hình 6a). Tính độ dài cạnh huyền BC theo a, rồi tính các tỉ số lượng giác của góc 45o .
b) Cho tam giác đều MNP có cạnh bằng a (Hình 6b). Tính độ dài đường cao MH theo a, rồi tính các tỉ số lượng giác của góc 30o và góc 60o .
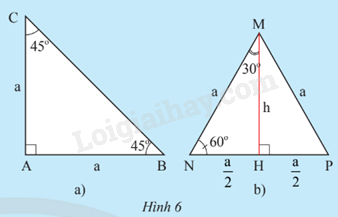
- Áp dụng định lý Pythagore vào tam giác vuông ABC để tính BC, tam giác vuông MHN để tính MH.
- Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \). Xét tam giác ABC vuông tại A có \(\widehat {ABC} = \alpha \) , ta có:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \).
a) Xét tam giác vuông cân ABC:
Áp dụng định lý Pythagore ta có:
BC = \(\sqrt {{a^2} + {a^2}} = a\sqrt 2 \).
Các tỉ số lượng giác của góc 45o là:
sin 45o = \(\frac{{AC}}{{BC}} = \frac{a}{{\sqrt 2 a}} = \frac{\sqrt 2 }{{ 2 }}\)
cos 45o = \(\frac{{AB}}{{BC}} = \frac{a}{{\sqrt 2 a}} = \frac{\sqrt 2 }{{ 2 }}\)
tan 45o = \(\frac{{AC}}{{AB}} = \frac{a}{a} = 1\)
cot 45o = \(\frac{1}{{\tan {{45}^o}}} = \frac{1}{1} = 1\)
b) Xét tam giác vuông MHN vuông tại H:
Áp dụng định lý Pythagore ta có:
MH = \(\sqrt {M{N^2} - M{H^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}a\).
Các tỉ số lượng giác của góc 30o là:
sin 30o = \(\frac{{NH}}{{NM}} = \frac{{\frac{a}{2}}}{a} = \frac{1}{2}\)
cos 30o = \(\frac{{MH}}{{NM}} = \frac{{\frac{{\sqrt 3 a}}{2}}}{a} = \frac{{\sqrt 3 }}{2}\)
tan 30o = \(\frac{{NH}}{{MH}} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{3}\)
cot 30o = \(\frac{1}{{\tan {{30}^o}}} = 1:\frac{{\sqrt 3 }}{3} = \sqrt 3 \)
Các tỉ số lượng giác của góc 60o là:
sin 60o = \(\frac{{MH}}{{NM}} = \frac{{\frac{{\sqrt 3 a}}{2}}}{a} = \frac{{\sqrt 3 }}{2}\)
cos 60o = \(\frac{{NH}}{{NM}} = \frac{{\frac{a}{2}}}{a} = \frac{1}{2}\)
tan 60o = \(\frac{{MH}}{{NH}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\frac{a}{2}}} = \sqrt 3 \)
cot 60o = \(\frac{1}{{\tan {{60}^o}}} = 1:\sqrt 3 = \frac{\sqrt 3}{{3 }}\)

Các bài tập cùng chuyên đề
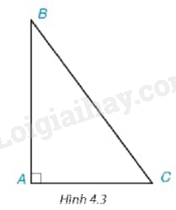
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat B = \widehat {B'} = \alpha .\) Chứng minh rằng:
a) \(\Delta ABC\backsim \Delta A'B'C';\)
b) \(\frac{{AC}}{{BC}} = \frac{{A'C'}}{{B'C'}};\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}};\frac{{AC}}{{AB}} = \frac{{A'C'}}{{A'B'}};\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, cosin, tang, cotang của các góc nhọn B và C khi biết:
a) AB = 8 cm, BC = 17 cm;
b) AC = 0,9 cm, AB = 1,2 cm.
Trong Hình 4.32, \(\cos \alpha \) bằng
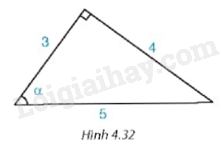
A. \(\frac{5}{3}.\)
B. \(\frac{3}{4}.\)
C. \(\frac{3}{5}.\)
D. \(\frac{4}{5}.\)
Trong tam giác MNP vuông tại M (H.4.33), \(\sin \widehat {MNP}\) bằng:
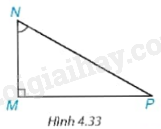
A. \(\frac{{PN}}{{MN}}\)
B. \(\frac{{MP}}{{PN}}\)
C. \(\frac{{MN}}{{PN}}\)
D. \(\frac{{MN}}{{MP}}\)
Trong tam giác ABC vuông tại A (H.4.34), \(\tan \widehat B\) bằng
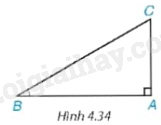
A. \(\frac{{AB}}{{AC}}\).
B. \(\frac{{AC}}{{AB}}\).
C. \(\frac{{AB}}{{BC}}\).
D. \(\frac{{BC}}{{AC}}\).
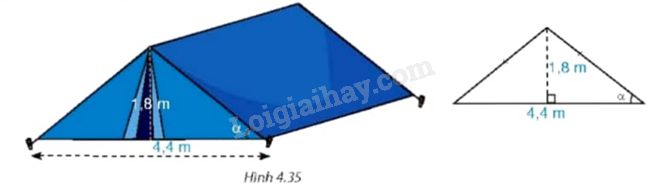
Hình 4.35 là mô hình của một túp lều. Tìm góc \(\alpha \) giữa cạnh mái lều và mặt đất (làm tròn kết quả đến phút).
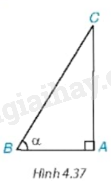
Cho tam giác ABC vuông tại A, có \(\widehat B = \alpha \) (H.4.37).
a) Hãy viết các tỉ số lượng giác \(\sin \alpha ;\cos \alpha \)
b) Sử dụng định lý Pythagore, chứng minh rằng \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
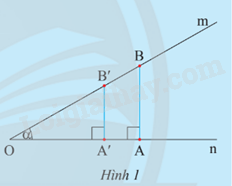
Cho góc nhọn \(\widehat {mOn} = \alpha \). Lấy hai điểm A và A’ trên On, kẻ hai đường thẳng qua A và A’ vuông góc với On và cắt Om lần lượt tại B và B’.
a) Có nhận xét gì về hai tam giác OAB và OA’B’?
b) So sánh các cặp tỉ số?
\(\frac{{AB}}{{OA}}\) và \(\frac{{A'B'}}{{OA'}}\); \(\frac{{AB}}{{OB}}\) và \(\frac{{A'B'}}{{OB'}}\); \(\frac{{OA}}{{OB}}\) và \(\frac{{OA'}}{{OB'}}\).
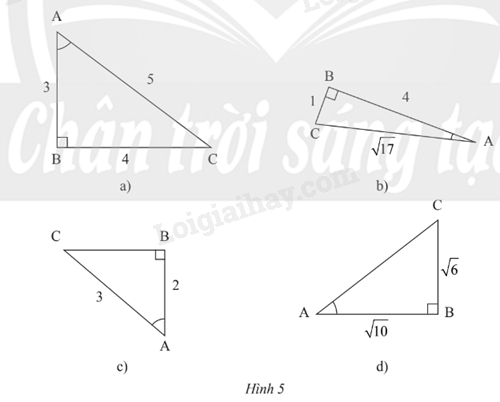
Tính các tỉ số lượng giác của góc nhọn A trong mỗi tam giác vuông ABC có \(\widehat B = {90^o}\) ở Hình 5 (kết quả làm tròn đến hàng phần trăm).
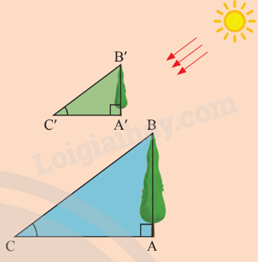
Sử dụng tỉ số lượng giác để giải thích tình huống trong Hoạt động khởi động (Trang 60).
Tại một thời điểm, khi những tia nắng chiếu, cây và bóng tạo thành các tam giác vuông như hình bên. Với \(\widehat C = \widehat {C'}\) , so sánh các tỉ số \(\frac{{AB}}{{AC}}\) và \(\frac{{A'B'}}{{A'C'}}\) .
Tính giá trị biểu thức sau:
a) A = \(\frac{{2\cos {{45}^o}}}{{\sqrt 2 }} + \sqrt 3 \tan {30^o}\)
b) B = \(\frac{{2\sin {{60}^o}}}{{\sqrt 3 }} - \cot {45^o}\)
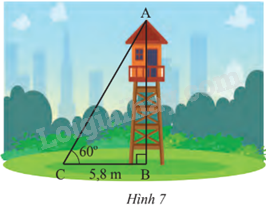
Tính chiều cao của tháp canh trong Hình 7 (kết quả làm tròn đến hàng phần trăm)
Cho tam giác ABC vuông tại A có BC = 8 cm, AC = 6 cm. Tỉ số lượng giác tan C (kết quả làm tròn đến hàng phần trăm) là
A. 0,87
B. 0,86
C. 0,88
D. 0,89
Cho tam giác ABC vuông tại A. Chứng minh rằng \(\frac{{AC}}{{AB}} = \frac{{\sin B}}{{\sin C}}\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = \alpha \) (Hình 2).
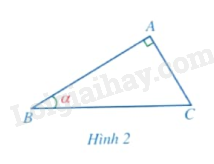
a) Cạnh góc vuông nào là cạnh đối của góc \(B\)?
b) Cạnh góc vuông nào là cạnh kề của góc \(B\)?
c) Cạnh nào là cạnh huyền?
Cho tam giác \(MNP\) vuông tại \(M,MN = 3cm,MP = 4cm\). Tính độ dài cạnh \(NP\) và các tỉ số lượng giác của góc \(P\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 4cm,BC = 6cm\). Tính các tỉ số lượng giác của góc \(B\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 2cm,AC = 3cm\). Tính các tỉ số lượng giác của góc \(C\).
Cho tam giác \(MNP\) có \(MN = 5cm,MP = 12cm,NP = 13cm\). Chứng minh tam giác \(MNP\) vuông tại \(N\). Từ đó, tính các tỉ số lượng giác của góc \(N\).
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và \(\widehat B = \alpha \) (Hình 40).
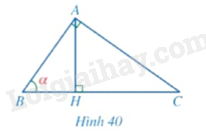
a) Tỉ số \(\frac{{HA}}{{HB}}\) bằng:
A. \(\sin \alpha \).
B. \(\cos \alpha \).
C. \(\tan \alpha \).
D. \(\cot \alpha \).
b) Tỉ số \(\frac{{HA}}{{HC}}\) bằng:
A. \(\sin \alpha \).
B. \(\cos \alpha \).
C. \(\tan \alpha \).
D. \(\cot \alpha \).
c) Tỉ số \(\frac{{HA}}{{AC}}\) bằng:
A. \(\sin \alpha \).
B. \(\cos \alpha \).
C. \(\tan \alpha \).
D. \(\cot \alpha \).
Theo quy chuẩn kĩ thuật quốc gia về xây dựng công trình đảm bảo cho người khuyết tật tiếp cận sử dụng (QCVN 10:2014/BXD), tỉ số giữa chiều cao h và chiều dài theo phương ngang d của dốc cho xe lăn không được lớn hơn \(\frac{1}{{12}}\) như Hình 4.1. Nếu góc nghiêng của một con dốc so với phương ngang là \(\alpha = {5^o}\) thì con dốc đó có đáp ứng được quy chuẩn trên không?

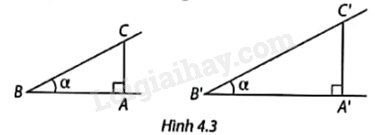
1. Vẽ một góc nhọn có số đo \(\alpha \) bất kì. Chọn một điểm C trên một cạnh và vẽ đường vuông góc CA từ C xuống cạnh còn lại (Hình 4.3). Hãy đo và tính các tỉ số cạnh đối và cạnh huyền, cạnh kề và cạnh huyền, cạnh đối và cạnh kề của góc B trong tam giác ABC.
2. Vẽ thêm một góc nhọn B’ cũng có số đo \(\alpha \) như trên và thực hiện tương tự.
3. Sử dụng dấu hiệu đồng dạng của hai tam giác vuông, hãy giải thích vì sao các cặp tỉ số tương ứng của \(\widehat B\) và \(\widehat {B'}\) bằng nhau.
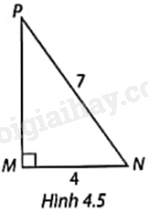
Tính các tỉ số lượng giác của góc N và góc P trong Hình 4.5.
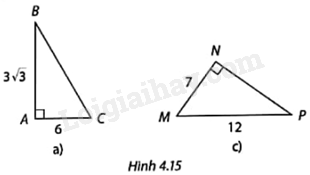
Tính số đo các góc nhọn của các tam giác vuông ở Hình 4.15.
Làm tròn số đo góc đến độ.
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
Tính số đo các góc nhọn của tam giác vuông, biết:
a) Tỉ số giữa hai cạnh góc vuông là \(\frac{5}{7}\);
b) Tỉ số giữa một cạnh góc vuông và cạnh huyền bằng \(\frac{2}{5}\).
Cho tam giác vuông có góc nhọn \(\alpha \). Tỉ số giữa cạnh đối và cạnh kề của góc \(\alpha \) là
A. \(\sin \alpha \).
B. \(\cos \alpha \).
C. \(\tan \alpha \).
D. \(\cot \alpha \).
Tam giác ABC vuông tại A có \(AB = 10cm,BC = 15cm\). Khi đó, sinB bằng
A. \(\frac{{\sqrt 5 }}{3}\).
B. \(\frac{{\sqrt 3 }}{5}\).
C. \(\frac{3}{5}\).
D. \(\frac{5}{3}\).
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$







Danh sách bình luận