Cho ∆DFE cân tại E. Gọi M là trung điểm của DF.
a) Chứng minh: $\Delta EDM{\rm{ }} = {\rm{ }}\Delta EFM$.
b) Chứng minh $EM \bot DF$.
c) Từ M vẽ MA $\bot$ ED tại A, MB $\bot$ EF tại B. Chứng minh AB // DF.

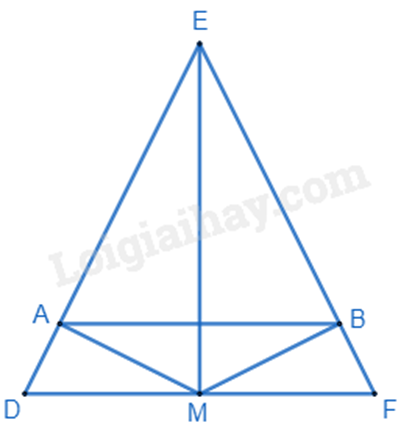
a) Xét $\Delta EDM$ và $\Delta EFM$ có:

DE = EF (tam giác DFE cân tại E)

DM = MF (M là trung điểm của DF)

ME chung

Suy ra $\Delta EDM = \Delta EFM$ (c.c.c) (đpcm)

b) $\Delta EDM = \Delta EFM$ suy ra $\widehat {EMD} = \widehat {EMF}$ (hai góc tương ứng)

Mà $\widehat {EMD}$ và $\widehat {EMF}$ là hai góc kề bù nên $\widehat {EMD} + \widehat {EMF} = {180^0}$

Suy ra $\widehat {EMD} = \widehat {EMF} = \frac{{{{180}^0}}}{2} = {90^0}$ hay $EM \bot DF$ (đpcm)

c) $\Delta EDM = \Delta EFM$ suy ra $\widehat {DEM} = \widehat {FEM}$ (hai góc tương ứng)

Xét $\Delta AEM$ và $\Delta BEM$ có:

$\widehat {AEM} = \widehat {BEM}$ (cmt)

$\widehat {EAM} = \widehat {EBM}\left( { = {{90}^0}} \right)$

EM chung

Suy ra $\Delta AEM = \Delta BEM$ (cạnh huyền – góc nhọn)

Suy ra AE = EB (hai cạnh tương ứng) suy ra $\Delta AEB$ là tam giác cân tại E.

$\widehat {EAB} = \widehat {EBA} = \frac{{{{180}^0} - \widehat E}}{2}$

Mà $\Delta DFE$ cân tại E nên $\widehat {EDF} = \widehat {EFD} = \frac{{{{180}^0} - \widehat E}}{2}$

Suy ra $\widehat {EAB} = \widehat {EDF}$.

Mà $\widehat {EAB}$ và $\widehat {EDF}$ là hai góc đồng vị nên AB // DF (đpcm)